ロボットモデリング

ロボットのデータ構造とモデリング

ロボットのデータ構造と順運動学

ロボットの構造はリンクと関節から構成されていると考えることが出来るが， ロボットを関節とリンクに分割する方法として

  • (a)切り離されるリンクの側に関節を含める
  • (b)胴体，あるいは胴体に近いほうに関節を含める

が考えられる．コンピュータのデータ構造を考慮し， (a)が利用されている．その理由は胴体以外のすべてのリンクにおいて， 必ず関節を一つ含んだ構造となり，すべてのリンクを同一のアルゴリズムで扱う ことが出きるためである．

この様に分割されたリンクを計算機上で表現するためにはツリー構造を利用する ことが出来る．一般的にはツリー構造を作るときに二分木にすることでデータ構 造を簡略化することが多い．

ロボットのリンクにおける同次変換行列の求め方としては，関節回転座標系上に 原点をもつ\(\Sigma_j\)を設定し，親リンク座標系からみた回転軸ベクトルが \(a_j\), \(\Sigma_j\)の原点が\(b_j\)であり，回転の関節角度を\(q_j\)とする．

このとき\(\Sigma_j\)の親リンク相対の同次変換行列は

\[ \begin{align}\begin{aligned}\begin{split} {}^iT_j = \left[ \begin{array}{cc} e^{\hat{a}_jq_j} & b_j \\ 0~0~0 & 1 \end{array} \right]\end{split}\\と書くことが出来る．\end{aligned}\end{align} \]

ここで，\(e^{\hat{a}_jq_j}\)は，一定速度の角速度ベクトルによって生ずる回 転行列を与える以下のRodriguesの式を用いている．これを回転軸\(a\)周りに \(wt[rad]\)だけ回転する回転行列を与えるものとして利用している．

\[e^{\hat{\omega}t} = E + \hat{a} sin (wt) + \hat{a}^2 (1 - cos(wt))\]

親リンクの位置姿勢\(p_i, R_i\)が既知だとすると，\(\Sigma_i\)の同次変換行列を

\[ \begin{align}\begin{aligned}\begin{split} T_i = \left[ \begin{array}{cc} R_i & p_i \\ 0~0~0 & 1 \end{array} \right]\end{split}\\と作ることができ，ここから\end{aligned}\end{align} \]
\[T_j = T_i ~ {}^iT_j\]

として計算できる．これをロボットのルートリンクから初めてすべてのリンクに 順次適用することでロボットの全身の関節角度情報から姿勢情報を算出すること ができ，これを順運動学と呼ぶ．

EusLispによる幾何情報のモデリング

Euslispの幾何モデリングでは，基本モデル(body)の生成，bodyの合成関数，複 合モデル(bodyset)の生成と3つの段階がある．

これまでに以下のような基本モデルの生成，合成が可能な事を見てきている．

(setq c1 (make-cube 100 100 100))
(send c1 :locate #f(0 0 50))
(send c1 :rotate (deg2rad 30) :x)
(send c1 :set-color :yellow)
(objects (list c1))

(setq c2 (make-cylinder 50 100))
(send c2 :move-to
      (make-coords
       :pos #f(20 30 40)
       :rpy (float-vector 0 0 (deg2rad 90)))
      :world)
(send c2 :set-color :green)
(objects (list c1 c2))

(setq c3 (body+ c1 c2))
(setq c4 (body- c1 c2))
(setq c5 (body* c1 c2))

bodysetはirteusで導入された複合モデルであり，bodyで扱えない複数の物体や 複数の色を扱うためのものである．

(setq c1 (make-cube 100 100 100))
(send c1 :set-color :red)
(setq c2 (make-cylinder 30 100))
(send c2 :set-color :green)
(send c1 :assoc c2)           ;;; これを忘れいように
(setq b1 (instance bodyset :init
                   (make-cascoords)
                   :bodies (list c1 c2)))
(objects (list b1))

幾何情報の親子関係を利用したサンプルプログラム

(setq c1 (make-cube 100 100 100))
(setq c2 (make-cube 50 50 50))
(send c1 :set-color :red)
(send c2 :set-color :blue)
(send c2 :locate #f(300 0 0))
(send c1 :assoc c2)
(objects (list c1 c2))
(do-until-key
 (send c1 :rotate (deg2rad 5) :z)
 (send *irtviewer* :draw-objects)
 (x::window-main-one) ;; process window event
 )

bodyset-linkとjointを用いたロボット（多リンク系）のモデリング

irteusではロボットリンクを記述するクラスとしてbodyset-link(irtmodel.l) というクラスが用意されている．これは機構情報と幾何情報をもち，一般的な木 構造でロボットの構造が表現されている．また，jointクラスを用いて関節情報 を扱っている．

(defclass bodyset-link
  :super bodyset
  :slots (joint parent-link child-links analysis-level default-coords
                weight acentroid inertia-tensor
                angular-velocity angular-acceleration
                spacial-velocity spacial-acceleration
                momentum-velocity angular-momentum-velocity
                momentum angular-momentum
                force moment ext-force ext-moment))

ジョイント（関節）のモデリングはjointクラス(irtmodel.l)を用いる．jointクラスは基底ク ラスであり，実際にはrotational-joint, linear-joint等を利用する． jointの子クラスで作られた関節は，:joint-angleメソッドで関節角度を指定す ることが出来る．

(defclass joint
  :super propertied-object
  :slots (parent-link child-link joint-angle min-angle max-angle
    default-coords))
(defmethod joint
  (:init (&key name
               ((:child-link clink)) ((:parent-link plink))
               (min -90) (max 90) &allow-other-keys)
         (send self :name name)
         (setq parent-link plink child-link clink
               min-angle min max-angle max)
         self))

(defclass rotational-joint
  :super joint
  :slots (axis))
(defmethod rotational-joint
  (:init (&rest args &key ((:axis ax) :z) &allow-other-keys)
         (setq axis ax joint-angle 0.0)
         (send-super* :init args)
         self)
  (:joint-angle
   (&optional v)
   (when v
        (setq relang (- v joint-angle) joint-angle v)
        (send child-link :rotate (deg2rad relang) axis)))
     joint-angle))

ここでは，joint, parent-link, child-links, defualt-coordsを利用する．

簡単な１関節ロボットの例としてサーボモジュールを作ってみると

(defun make-servo nil
  (let (b1 b2)
    (setq b1 (make-cube 35 20 46))
    (send b1 :locate #f(9.5 0 0))
    (setq b2 (make-cylinder 3 60))
    (send b2 :locate #f(0 0 -30))
    (setq b1 (body+ b1 b2))
    (send b1 :set-color :gray20)
    b1))

(defun make-hinji nil
  (let ((b2 (make-cube 22 16 58))
        (b1 (make-cube 26 20 54)))
    (send b2 :locate #f(-4 0 0))
    (setq b2 (body- b2 b1))
    (send b1 :set-color :gray80)
    b2))

(setq h1 (instance bodyset-link :init (make-cascoords) :bodies (list (make-hinji))))
(setq s1 (instance bodyset-link :init (make-cascoords) :bodies (list (make-servo))))
(setq j1 (instance rotational-joint :init :parent-link h1 :child-link s1 :axis :z))
;; instance cascaded coords
(setq r (instance cascaded-link :init))
(send r :assoc h1)
(send h1 :assoc s1)
(setq (r . links) (list h1 s1))
(setq (r . joint-list) (list j1))
(send r :init-ending)

となる．

ここでは，h1，s1というbodyset-linkと， j1というrotational-jointを作成し，ここから cascaded-linkという，連結リンクからなるモデルを生成している． cascaded-linkはcascaded-coordsの子クラスであるため， r (cascaded-link)，h1，s1の座標系の親子関係を :assocを利用して設定している．

(r . links)という記法はrというオブジェクトのスロット変数 （メンバ変数）であるlinksにアクセスしている．ここでは， linksおよびjoint-listに適切な値をセットし， (send r :init-ending)として必要な初期設定を行っている．

これでrという2つのリンクと１つの関節情報 を含んだ1つのオブジェクトを生成できる．これで例えば (objects (list h1 s1))ではなく， (objects (list r))としてロボットをビューワに表示できる． また，(send r :locate #f(100 0 0))などの利用も可能になっている．

cascaded-linkクラスのメソッドの利用例としては以下ある． :joint-list，:linksといった関節リストやリンクリストへの アクセサに加え，関節角度ベクトルへのアクセスを提供する :angle-vectorメソッドが重要である．これを引数なしで呼び出せば現 在の関節角度が得られ，これに関節角度ベクトルを引数に与えて呼び出せば，その引 数が示す関節角度ベクトルをロボットモデルに反映させることができる．

$ (objects (list r))
(#<servo-model #X628abb0  0.0 0.0 0.0 / 0.0 0.0 0.0>)
;; useful cascaded-link methods
$ (send r :joint-list)
(#<rotational-joint #X6062990 :joint101067152>)
$ (send r :links)
(#<bodyset-link #X62ccb10 :bodyset103598864  0.0 0.0 0.0 / 0.0 0.0 0.0>
 #<bodyset-link #X6305830 :bodyset103831600  0.0 0.0 0.0 / 0.524 0.0 0.0>)
$ (send r :angle-vector)
#f(0.0)
$ (send r :angle-vector (float-vector 30))
#f(30.0)

EusLispにおける順運動学計算

順運動学計算を行うには，cascaded-corods, bodyset, bodyset-link 各クラ スに定義された :worldcoords メソッドを用いる． :worldcoords メソッドは，ルートリンクが見つかる（親リンクがなくなる） か， スロット変数 changed が nil であるリンク （一度順運動学計算を行ったことがある）が見つかるまで さかのぼって親リンクの :worldcoords メソッドを呼び出すことで 順運動学計算を行う． その際，スロット変数 changed を nil で上書く． したがって，二度目の :worldcoords メソッドの呼び出しでは，一度計算され たリンクの順運動学計算は行われず，即座にリンクの位置姿勢情報を取り出す ことができる．

また，bodyset-link クラスの :worldcoords メソッドは, level 引数を取る ことができ，それが :coords である場合には，リンクのもつ bodies スロット変数 の順運動学計算は行われない． bodies にリンクの頂点を構成する faceset が含まれている場合には，これら についての順運動学計算を省略することで大幅な高速化が期待できるだろう． なお， level 引数の初期値には，リンクのもつ analysis-level スロット変数 が用いられるため，常に bodies の順運動学計算を行わない場合は， リンクのインスタンス l について (send l :analysis-level :coords) とすればよい．

(defmethod bodyset-link
  (:worldcoords
   (&optional (level analysis-level))
   (case
    level
    (:coords (send-message self cascaded-coords :worldcoords))
    (t       (send-super :worldcoords)))
   ))

(defmethod bodyset
  (:worldcoords
   ()
   (when changed
     (send-super :worldcoords)
     (dolist (b bodies) (send b :worldcoords)))
   worldcoords))

(defmethod cascaded-coords
 (:worldcoords  ()      ;calculate rot and pos in the world
   (when changed
      (if parent
          (transform-coords (send parent :worldcoords) self
worldcoords)
          (send worldcoords :replace-coords self))
      (send self :update)
      (setf changed nil))
   worldcoords))

ロボットの動作生成

逆運動学

逆運動学においては, エンドエフェクタの位置・姿勢\(^0_n\bm{H}\)から マニピュレータの関節角度ベクトル \(\bm{\theta}=(\theta_1, \theta_2, ..., \theta_n)^T\) を求める.

ここで, エンドエフェクタの位置・姿勢\(\bm{r}\) は関節角度ベクトルを用いて

\[ \begin{align}\begin{aligned} \begin{aligned} \bm{r} = \bm{f}(\bm{\theta}) \eqlabel{forward-kinematics-functional}\end{aligned}\\とかける. は のように記述し,関節角度ベクトルを求める.\end{aligned}\end{align} \]
\[\begin{aligned} \bm{\theta} = \bm{f}^{-1}(\bm{r}) \eqlabel{inverse-kinematics-func}\end{aligned}\]

における\(f^{-1}\)は一般に非線形な関数となる. そこでを時刻tに関して微分することで, 線形な式

\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} \dot{\bm{r}} &=& \frac{\partial \bm{f}}{\partial \bm{\theta}} (\bm{\theta})\dot{\bm{\theta}} \\ &=& \bm{J}(\bm{\theta})\dot{\bm{\theta}} \eqlabel{inverse-kinematics-base}\end{aligned}\end{split}\\を得る. ここで,\end{aligned}\end{align} \]

\(\bm{J}(\bm{\theta})\)は\(m \times n\)のヤコビ行列である. \(m\)はベクトル\(\bm{r}\)の次元, \(n\)はベクトル\(\bm{\theta}\)の次元である. \(\bm{\dot{r}}\)は速度・角速度ベクトルである.

ヤコビ行列が正則であるとき逆行列\(\bm{J}(\bm{\theta})^{-1}\)を用いて 以下のようにしてこの線型方程式の解を得ることができる.

\[\begin{aligned} \dot{\bm{\theta}} = \bm{J}(\bm{\theta})^{-1}\dot{\bm{r}} \eqlabel{inverse-kinematics}\end{aligned}\]

しかし, 一般にヤコビ行列は正則でないので, ヤコビ行列の疑似逆行列\(\bm{J}^{\#}(\bm{\theta})\) が用いられる().

\[\begin{split}\begin{aligned} \bm{A}^{\#} = \left\{ \begin{array}{l l} & \bm{A}^{-1} \ ( m = n = rank \bm{A}) \\ & \bm{A}^T \ (\bm{A}\bm{A}^T)^{-1} ( n > m = rank \bm{A}) \\ & (\bm{A}^T\bm{A})^{-1}\bm{A}^T \ ( m > n = rank \bm{A}) \end{array} \right. \eqlabel{psuedo-inverse-matrix}\end{aligned}\end{split}\]

は， \(m>n\)のときはを， \(n>=m\)のときはを， 最小化する最小二乗解を求める問題と捉え,解を得る.

\[\begin{aligned} \min_{\dot{\bm{\theta}}} \left(\dot{\bm{r}} - \bm{J}(\bm{\theta})\dot{\bm{\theta}}\right)^{T} \left(\dot{\bm{r}} - \bm{J}(\bm{\theta})\dot{\bm{\theta}}\right) \eqlabel{inverse-kinematics-error-func}\end{aligned}\]
\[\begin{split}\begin{aligned} \min_{\dot{\bm{\theta}}} & \dot{\bm{\theta}}^{T}\dot{\bm{\theta}}\\ \nonumber s.t. & \dot{\bm{r}} = \bm{J}(\bm{\theta})\dot{\bm{\theta}} \eqlabel{inverse-kinematics-min-func}\end{aligned}\end{split}\]

関節角速度は次のように求まる．

\[\begin{aligned} \dot{\bm{\theta}} = \bm{J}^{\#}(\bm{\theta})\dot{\bm{r}} + \left(\bm{E}_n - \bm{J}^{\#}(\bm{\theta})\bm{J}(\bm{\theta})\right)\bm{z} \eqlabel{inverse-kinematics-lagrangian-formula}\end{aligned}\]

しかしながら, に従って解を 求めると, ヤコビ行列\(\bm{J}(\bm{\theta})\)がフルランクでなくなる特異点に近づく と, \(\left|\dot{\bm{\theta}}\right|\)が大きくなり不安定な振舞いが生じる. そこで, Nakamura et al.のSR-Inverse [1] を用いること で, この特異点を回避する.

本研究では ヤコビ行列の疑似逆行列\(\bm{J}^{\#}(\bm{\theta})\)の代わりに, に示す\(\bm{J}^{*}(\bm{\theta})\) を用いる.

\[\begin{aligned} \bm{J}^{*}(\bm{\theta}) = \bm{J}^T\left(\bm{J}\bm{J}^T + \epsilon \bm{E}_m\right)^{-1} \eqlabel{SR-inverse-jacobian}\end{aligned}\]

これは, の代わりに, を最小化する最適化問題を 解くことにより得られたものである.

\[\begin{aligned} \min_{\dot{\bm{\theta}}} \{ \dot{\bm{\theta}}^T \dot{\bm{\theta}} + \epsilon \left(\dot{\bm{r}} - \bm{J}(\bm{\theta})\dot{\bm{\theta}}\right)^T \left(\dot{\bm{r}} - \bm{J}(\bm{\theta})\dot{\bm{\theta}}\right) \} \eqlabel{SR-inverse-error-func}\end{aligned}\]

ヤコビ行列\(\bm{J}(\bm{\theta})\)が特異点に近づいているかの指標には 可操作度\(\kappa(\bm{\theta})\) [2] が用いられる().

\[\begin{aligned} \kappa(\bm{\theta}) = \sqrt{\bm{J}(\bm{\theta}) \bm{J}^{T}(\bm{\theta})} \eqlabel{manipulability}\end{aligned}\]

微分運動学方程式における タスク空間次元の選択行列 [3] は見通しの良い定式化のために省略するが, 以降で導出する全ての式において 適用可能であることをあらかじめことわっておく.

基礎ヤコビ行列

一次元対偶を関節に持つマニピュレータのヤコビアンは 基礎ヤコビ行列 [4] により 計算することが可能である. 基礎ヤコビ行列の第\(j\)関節に対応するヤコビアンの列ベクトル\(\bm{J}_j\)は

\[\begin{split}\bm{J}_j= \begin{cases} \left[ \begin{array}{ccc} \bm{a}_j\\ \bm{0} \end{array} \right] & \text{if linear joint} \\ \left[ \begin{array}{ccc} \bm{a}_j \times (\bm{p}_{end} - \bm{p}_j)\\ \bm{a}_j \end{array} \right] & \text{if rotational joint} \end{cases}\end{split}\]

と表される. \(\bm{a}_j\)・\(\bm{p}_j\)はそれぞれ第\(j\)関節の関節軸単位ベクトル・位置ベクトルであり, \(\bm{p}_{end}\)はヤコビアンで運動を制御するエンドエフェクタの位置ベクトルである. 上記では1自由度対偶の 回転関節・直動関節について導出したが， その他の関節でもこれらの列ベクトルを 連結した行列としてヤコビアンを定義可能である． 非全方位台車の運動を表す2自由度関節は 前後退の直動関節と 旋回のための回転関節から構成できる． 全方位台車の運動を表す3自由度関節は 並進2自由度の直動関節と 旋回のための回転関節から構成できる． 球関節は姿勢を姿勢行列で， 姿勢変化を等価角軸変換によるものとすると， 3つの回転関節をつなぎ合わせたものとみなせる．

関節角度限界回避を含む逆運動学

ロボットマニピュレータの軌道生成において, 関節角度限界を考慮することはロボットによる実機実験の際に重要となる. 本節では,文献 [5] [6] の式および文章を引用しつつ, 関節角度限界の回避を 含む逆運動学について説明する.

重み付きノルムを以下のように定義する.

\[\begin{aligned} \left|\bm{\dot{\theta}}\right|_{\bm{W}} = \sqrt{\bm{\dot{\theta}}^T\bm{W}\bm{\dot{\theta}}} \eqlabel{weighted-norm}\end{aligned}\]

ここで, \(\bm{W}\)は\(\bm{W} \in \bm{R}^{n \times n}\)であり, 対象で全ての要 素が正である重み係数行列である. この\(\bm{W}\)を用いて, \(\bm{J}_{\bm{W}}, \bm{\dot{\theta}}_{\bm{W}}\)を以下のよう に定義する.

\[\begin{aligned} \bm{J}_{\bm{W}} = \bm{J}\bm{W}^{-\frac{1}{2}}, \bm{\dot{\theta}}_{\bm{W}} = \bm{W}^{\frac{1}{2}}\bm{\dot{\theta}}\end{aligned}\]

この\(\bm{J}_{\bm{W}}, \bm{\dot{\theta}}_{\bm{W}}\)を用いて, 以下の式を得 る.

\[\begin{split}\begin{aligned} \dot{\bm{r}} & = & \bm{J}_{\bm{W}}\bm{\dot{\theta}}_{\bm{W}} \\ \left|\dot{\bm{\theta}}\right|_{\bm{W}} & = & \sqrt{\bm{\dot{\theta}}_{\bm{W}}^T\bm{\dot{\theta}}_{\bm{W}}}\end{aligned}\end{split}\]

これによって線型方程式の解はから 以下のように記述できる.

\[\begin{aligned} \bm{\dot{\theta}}_{\bm{W}} = \bm{W}^{-1}\bm{J}^T \left(\bm{J}\bm{W}^{-1}\bm{J}^T\right)^{-1}\dot{\bm{r}}\end{aligned}\]

また、現在の関節角度\(\theta\)が関節角度限界\(\theta_{i,\max}, \theta_{i, \min}\)に対してどの程度余裕があるかを評価する ための関数\(H(\bm{\theta})\)は以下のようになる [7]).

\[\begin{aligned} H(\bm{\theta}) = \sum_{i = 1}^n\frac{1}{4} \frac{(\theta_{i,\max} - \theta_{i,\min})^2} {(\theta_{i,\max} - \theta_i)(\theta_i - \theta_{i,\min})} \eqlabel{joint-performance-func}\end{aligned}\]

次にに示すような\(n \times n\)の重み係数行列 \(\bm{W}\)を考える.

\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} \bm{W} = \left[ \begin{array}{ccccc} w_1 & 0 & 0 & \cdots & 0 \\ 0 & w_2 & 0 & \cdots & 0 \\ \cdots & \cdots & \cdots & \ddots & \cdots \\ 0 & 0 & 0 & \cdots & w_n \\ \end{array} \right] \eqlabel{joint-weight-matrix}\end{aligned}\end{split}\\ここで\ :math:`w_i`\ は\end{aligned}\end{align} \]
\[ \begin{align}\begin{aligned} \begin{aligned} w_i = 1 + \left|\frac{\partial \bm{H}(\bm{\theta})}{\partial \theta_i}\right|\end{aligned}\\である.\end{aligned}\end{align} \]

さらにから次の式を得る.

\[\begin{aligned} \frac{\partial H(\bm{\theta})}{\partial \theta_i} = \frac{(\theta_{i,\max} - \theta_{i,\min})^2(2\theta_i - \theta_{i,\max} - \theta_{i,\min})} {4(\theta_{i,\max} - \theta_i)^2(\theta_i - \theta_{i,\min})^2}\end{aligned}\]

関節角度限界から遠ざかる向きに関節角度が動いている場合には重み係数行列を 変化させる必要はないので,\(w_i\)を以下のように定義しなおす.

\[\begin{split}\begin{aligned} w_i = \left\{ \begin{array}{l l} 1 + \left|\frac{\partial \bm{H}(\bm{\theta})}{\partial \theta_i}\right| & if \;\Delta\left|\frac{\partial \bm{H}(\bm{\theta})}{\partial \theta_i}\right| \geq 0 \\ 1 & if \;\Delta\left|\frac{\partial \bm{H}(\bm{\theta})}{\partial \theta_i}\right| < 0 \end{array} \right.\end{aligned}\end{split}\]

この\(w_i\)および\(\bm{W}\)を用いることで関節角度限界回避を含む逆運動学を解くこ とができる.

衝突回避を含む逆運動学

ロボットの動作中での自己衝突や環境モデルとの衝突は 幾何形状モデルが存在すれば計算することが可能である. ここではSugiura et al. により提案されている効率的な衝突回避計算 [8] [9] を応用した動作生成法を示す. 実際の実装はSugiura et al. の手法に加え, タスク作業空間のNullSpaceの利用を係数により制御できるようにした点や 擬似逆行列ではなくSR-Inverseを用いて特異点に ロバストにしている点などが追加されている.

衝突回避のための関節角速度計算法

逆運動学計算における目標タスクと衝突回避の統合は リンク間最短距離を用いたblending係数により行われる. これにより,衝突回避の必要のないときは目標タスクを厳密に満し 衝突回避の必要性があらわれたときに目標タスクを あきらめて衝突回避の行われる関節角速度計算を行うことが可能になる. 最終的な関節角速度の関係式はで得られる. 以下では\(ca\)の添字は衝突回避計算のための成分を表し, \(task\)の部分は衝突回避計算以外のタスク目標を表すことにする.

\[\labeq{collision-avoidance-all} \bm{\dot{\theta}} = f(d)\bm{\dot{\theta}}_{ca} + \left(1-f(d)\right)\bm{\dot{\theta}}_{task}\]

blending係数\(f(d)\)は, リンク間距離\(d\)と閾値\(d_a\)・\(d_b\)の関数として計算される ().

\[\begin{split}\begin{aligned} \labeq{collision-avoidance-blending-coefficient} f(d) = \left\{ \begin{array}{l l} (d-d_a)/(d_b-d_a) & if d<d_a\\ 0 & otherwise \end{array} \right.\end{aligned}\end{split}\]

\(d_a\)は衝突回避計算を行い始める値 (yellow zone)であり, \(d_b\)は目標タスクを阻害しても衝突回避を行う閾値 (orange zone)である.

衝突計算をする2リンク間の最短距離・最近傍点が計算できた場合の 衝突を回避するための動作戦略は 2リンク間に作用する仮想的な反力ポテンシャルから導出される.

2リンク間の最近傍点同士をつなぐベクトル\(\bm{p}\)を用いた 2リンク間反力から導出される速度計算を に記す.

\[\begin{split}\begin{aligned} \labeq{collision-avoidance-distance-force} \bm{\delta x} = \left\{ \begin{array}{l l} 0 & if \left|\bm{p}\right|>d_{a}\\ (d_{a}/\left|\bm{p}\right|-1)\bm{p} & else \end{array} \right.\end{aligned}\end{split}\]

これを用いた関節角速度計算は となる.

\[\labeq{collision-avoidance-joint-speed} \dot{\bm{\theta}}_{ca} = \bm{J}_{ca}^{T} k_{joint} \bm{\delta x} + (\bm{E}_n - \bm{J}_{task}^{*}\bm{J}_{task}) \bm{J}_{ca}^{T} k_{null} \bm{\delta x}\]

\(k_{joint}\)・\(k_{null}\)はそれぞれ反力ポテンシャルを 目標タスクのNullSpaceに分配するかそうでないかを制御する係数である.

衝突回避計算例

以下ではロボットモデル・環境モデルを用いた衝突回避例を示す. 本研究では, ロボットのリンク同士,またはリンクと物体の衝突判定には,衝突判定ライブラリ PQP(A Proximity Query Package) [10]_を用いた.

では \(d_a = 200[mm]\),\(d_b = 0.1 * d_a = 20[mm]\), \(k_{joint} = k_{null} = 1.0\)と設定した.

この衝突判定計算では,衝突判定をリンクの設定を

  1. リンクのリスト\(n_{ca}\)を登録
  2. 登録されたリンクのリストから全リンクのペア\(_{n_{ca}}C_2\)を計算
  3. 隣接するリンクのペア,常に交わりを持つリンクのペアなどを除外

のように行うという工夫を行っている.

例では衝突判定をするリンクを 「前腕リンク」「上腕リンク」「体幹リンク」「ベースリンク」 の4つとして登録した. この場合, \(_4C_2\)通りのリンクのペア数から 隣接するリンクが除外され,全リンクペアは 「前腕リンク-体幹リンク」 「前腕リンク-ベースリンク」 「上腕リンク-ベースリンク」 の3通りとなる.

の3本の線(赤1本,緑2本)が 衝突形状モデル間での最近傍点同士をつないだ 最短距離ベクトルである. 全リンクペアのうち赤い線が最も距離が近いペアであり, このリンクペアより衝突回避のための 逆運動学計算を行っている.

Example of Collision Avoidance

Example of Collision Avoidance

非ブロック対角ヤコビアンによる全身協調動作生成

ヒューマノイドは枝分かれのある複雑な構造を持ち, 複数のマニピュレータで協調して動作を行う必要がある ()．

Duplicate Link Sequence Duplicate Link Sequence

複数マニピュレータの動作例として,

  • リンク間に重複がない場合
    それぞれのマニピュレータについて 式を用いて関節角速度を求める. もしくは,複数の式を連立した方程式(ヤコビアンはブロック対角行列となる) を用いて関節角速度を求めても良い.
  • リンク間に重複がある場合
    リンク間に重複がある場合は, リンク間の重複を考慮したヤコビアンを考える必要がある. 例えば,双腕動作を行う場合,左腕のマニピュレータのリンク系列と 右腕のマニピュレータのリンク系列とで,体幹部リンク系列が重複し, その部位は左右で協調して関節角速度を求める必要がある.

次節ではリンク間に重複がある場合の 非ブロック対角なヤコビアンの計算法 および それを用いた関節角速度計算法を述べる (前者の重複がない場合も以下の計算方法により後者の一部として計算可能で ある).

リンク間重複があるヤコビアン計算と関節角度計算

微分運動学方程式を求める際の条件を以下に示す.

  • マニピュレータの本数　\(L\)本

  • 全関節数　\(N\)個

  • マニピュレータの先端速度・角速度ベクトル \([\bm{\xi}_0^T,...,\bm{\xi}_{L-1}^T]^T\)

  • 各関節角速度ベクトル \([\bm{\dot{\theta}_0}^T,...,\bm{\dot{\theta}_{L-1}}^T]^T\)

  • 関節の添字和集合　\(S = \{0,\hdots,N-1\}\)
    ただし,マニピュレータ\(i\)の添字集合\(S_i\)を用いて\(S\)は \(S = S_0 \cup \hdots \cup S_{L-1}\)と表せる.

  • \(S\)に基づく関節速度ベクトル　\([\dot{\theta}_0, ..., \dot{\theta}_{N-1}]^T\)

とする.

運動学関係式はのようになる.

\[\begin{split}\begin{aligned} \left[ \begin{array}{c} \bm{\xi}_0 \\ \vdots\\ \bm{\xi}_{L-1} \end{array} \right] = \left[ \begin{array}{ccc} \bm{J}_{0,0} & \hdots & \bm{J}_{0, N-1}\\ \vdots & \bm{J}_{i,j} & \vdots\\ \bm{J}_{L-1,0} & \hdots & \bm{J}_{L-1, N-1} \end{array} \right] \left[ \begin{array}{c} \dot{\theta}_0\\ \vdots\\ \dot{\theta}_{N-1} \end{array} \right] \labeq{multi-manipulator-jacobi-eq}\end{aligned}\end{split}\]

小行列\(\bm{J}_{i,j}\)は以下のように求まる.

_i,j= _j & if \(j\)-th joint \(\in\) \(i\)-th link array
& otherwise

ここで，\(\bm{J}_j\)はのもの．

を単一のマニピュレータの 逆運動学解法と同様にSR-Inverseを用いて関節角速度を 求めることができる.

ここでの非ブロック対角ヤコビアンの計算法は, アーム・多指ハンドの動作生成
[11]_に おいて登場する運動学関係式から求まるヤコビアンを

導出することが可能である.

ベースリンク仮想ジョイントを用いた全身逆運動学法

一般に関節数が\(N\)であるのロボットの運動を表現するためには ベースリンクの位置姿勢と関節角自由度を合わせた\(N+6\)個の変数が必要であ る． ベースリンクとなる位置姿勢の変数を用いたロボットの運動の定式化は 宇宙ロボット [12]_だけでなく, 環境に固定されないヒューマノイドロボット

[13]_の場合にも重要である.

ここでは 腕・脚といったマニピュレータに ベースリンクに3自由度の直動関節と 3自由度の回転関節が仮想的に付随したマニピュレータ構成を考える (). 上記の仮想的な6自由度関節を 本研究ではベースリンク仮想ジョイントと名づける. ベースリンク仮想ジョイントを用いることにより ヒューマノイドの腰が動き全身関節が駆動され, 運動学,ひいては動力学的な解空間が拡充されることが期待できる.

|Concept of the Virtual Joint of the Base Link (Left figure) Overview of the Robot Model (Right figure) Skeleton Figure of Robot Model with the Virtual Joint | |Concept of the Virtual Joint of the Base Link (Left figure) Overview of the Robot Model (Right figure) Skeleton Figure of Robot Model with the Virtual Joint |

ベースリンク仮想ジョイントヤコビアン

ベースリンク仮想ジョイントのヤコビアンは 基礎ヤコビ行列の計算() を利用し， 絶対座標系\(x\)，\(y\)，\(z\)軸の直動関節と 絶対座標系\(x\)，\(y\)，\(z\)軸回りの回転関節を それぞれ連結した\(6\times6\)行列である． ちなみに,並進・回転成分のルートリンク仮想ジョイントのヤコビアンは 以下のように書き下すこともできる.

\[\begin{split}\begin{aligned} \labeq{virtual-joint-jacobian} \bm{J}_{B,l} = \left[ \begin{array}{cc} \bm{E}_3 & -\hat{\bm{p}}_{B\to l}\\ \bm{0} & \bm{E}_3 \end{array} \right]\end{aligned}\end{split}\]

\(\bm{p}_{B\to l}\)はベースリンク位置から添字\(l\)で表現する位置までの 差分ベクトルである．

マスプロパティ計算

複数の質量・重心・慣性行列を統合し 単一の質量・重心・慣性行列の組 \([m_{new}, \bm{c}_{new}, \bm{I}_{new}]\) を計算する演算関数を次のように定義する．

\[ \begin{align}\begin{aligned} [m_{new}, \bm{c}_{new}, \bm{I}_{new}] = AddMassProperty( [m_{1}, \bm{c}_{1}, \bm{I}_{1}] ,\hdots, [m_{K}, \bm{c}_{K}, \bm{I}_{K}] )\\これは次のような演算である．\end{aligned}\end{align} \]
\[m_{new} = \sum_{j=1}^{K}m_{j}\]
\[\bm{c}_{new} = \frac{1}{m_{new}}\sum_{j=1}^{K} m_j \bm{c}_j\]
\[ \begin{align}\begin{aligned} \bm{I}_{new} = \sum_{j=1}^{K} \left( \bm{I}_j + m_j \bm{D}(\bm{c}_{j} - \bm{c}_{new}) \right)\\ここで，\ :math:`\bm{D}(\bm{r})=\hat{\bm{r}}^T\hat{\bm{r}}`\ とする．\end{aligned}\end{align} \]

運動量・角運動量ヤコビアン

シリアルリンクマニピュレータを対象とし， 運動量・角運動量ヤコビアンを導出する． 運動量・原点まわりの角運動量を各関節変数で表現し， その偏微分でヤコビアンの行を計算する．

第\(j\)関節の運動変数を\(\theta_j\)とする． まず，回転・並進の1自由度関節を考える．

_j =

cl _j _j (_j - _j) _j &
_j _j _j &

_j =

cl _j _j + _j _j _j &
&

ここで， \([\tilde{m}_j, \tilde{\bm{c}}_j, \tilde{\bm{I}}_j]\)は AddMassProperty関数に第\(j\)関節の子リンクより 末端側のリンクのマスプロパティを与えたものであり， 実際には再帰計算により計算する [14]． これらを\(\dot{\theta}_j\)で割ることにより ヤコビアンの各列ベクトルを得る．

_j =

cl _j (_j - _j) _j &
_j _j &

_j =

cl _j _j + _j _j &
&

これより慣性行列は次のように計算できる．

\[\bm{M}_{\dot{\bm{\theta}}} = [\bm{m}_1, \hdots, \bm{m}_{N}]\]
\[ \begin{align}\begin{aligned} \bm{H}_{\dot{\bm{\theta}}} = [\bm{h}_1, \hdots, \bm{h}_{N}] - \hat{\bm{p}}_{G} \bm{M}_{\dot{\bm{\theta}}}\\ここでは，全関節数を\ :math:`N`\ とした． また，ベースリンクは\end{aligned}\end{align} \]

直動関節\(x\)，\(y\)，\(z\)軸， 回転関節\(x\)，\(y\)，\(z\)軸を もつと考え整理し，次のようになる．

\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} \left[ \begin{array}{c} \bm{M}_{B}\\ \bm{H}_{B} \end{array} \right] = \left[ \begin{array}{cc} M_{r} \bm{E}_3 & - M_{r} \hat{\bm{p}}_{B\to G}\\ \bm{0} & \tilde{\bm{I}} \end{array} \right]\end{aligned}\end{split}\\これを用いて重心まわりの角運動量・運動量は次のようになる．\end{aligned}\end{align} \]
\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} \left[ \begin{array}{c} \bm{P}\\ \bm{L} \end{array} \right] = \left[ \begin{array}{cc} \bm{M}_{B} & \bm{M}_{\dot{\bm{\theta}}}\\ \bm{H}_{B} & \bm{H}_{\dot{\bm{\theta}}} \end{array} \right] \left[ \begin{array}{c} \bm{\xi}_{B}\\ \dot{\bm{\theta}} \end{array} \right]\end{aligned}\end{split}\\ここで ヒューマノイドの全質量\ :math:`M_{r}`\ ，\end{aligned}\end{align} \]

重心位置\(\bm{p}_{G}\)， 慣性テンソル\(\tilde{\bm{I}}\)は次のように 全リンクのマスプロパティ演算より求める．

\[[M_{r}, \bm{p}_{G}, \tilde{\bm{I}}] = AddMassProperty( [m_{1}, \bm{c}_{1}, \bm{I}_{1}] ,\hdots, [m_{N}, \bm{c}_{N}, \bm{I}_{N}] )\]

重心ヤコビアン

重心ヤコビアンは 重心速度と関節角速度の間のヤコビアンである． 本論文ではベースリンク仮想ジョイントを用いるため， ベースリンクに6自由度関節がついたと考え ベースリンク速度角速度・関節角速度の 重心速度に対するヤコビアンを重心ヤコビアンとして用いる． 具体的には， ベースリンク成分\(\bm{M}_{B}\)と 使用関節について抜き出した成分\(\bm{M}_{\dot{\bm{\theta}}}^{\prime}\) による運動量ヤコビアンを 全質量で割ることで重心ヤコビアンを計算する．

\[\bm{J}_{G} = \frac{1}{M_{r}} \left[ \begin{array}{cc} \bm{M}_{B} & \bm{M}_{\dot{\bm{\theta}}}^{\prime} \end{array} \right]\]

ロボットの動作生成プログラミング

三軸関節ロボットを使ったヤコビアン，逆運動学の例

3軸関節をもつロボットを定義し， 逆運動学やヤコビアンの計算例を紹介する．

ロボットの定義は以下の用になる．

(defclass 3dof-robot
  :super cascaded-link
  :slots (end-coords l1 l2 l3 l4 j1 j2 j3))
(defmethod 3dof-robot
  (:init ()
   (let (b)
     (send-super :init)

     (setq b (make-cube 10 10 20))
     (send b :locate #f(0 0 10))
     (send b :set-color :red)
     (setq l4 (instance bodyset-link :init (make-cascoords) :bodies (list b) :name 'l4))
     (setq end-coords (make-cascoords :pos #f(0 0 20)))
     (send l4 :assoc end-coords)
     (send l4 :locate #f(0 0 100))
     ;;
     (setq b (make-cube 10 10 100))
     (send b :locate #f(0 0 50))
     (send b :set-color :green)
     (setq l3 (instance bodyset-link :init (make-cascoords) :bodies (list b) :name 'l3))
     (send l3 :assoc l4)
     (send l3 :locate #f(0 0 100))
     ;;
     (setq b (make-cube 10 10 100))
     (send b :locate #f(0 0 50))
     (send b :set-color :blue)
     (setq l2 (instance bodyset-link :init (make-cascoords) :bodies (list b) :name 'l2))
     (send l2 :assoc l3)
     (send l2 :locate #f(0 0 20))
     ;;
     (setq b (body+ (make-cube 10 10 20 :pos #f(0 0 10)) (make-cube 300 300 2)))
     (send b :set-color :white)
     (setq l1 (instance bodyset-link :init (make-cascoords) :bodies (list b) :name 'l1))
     (send l1 :assoc l2)
     ;;
     (setq j1 (instance rotational-joint :init :name 'j1
                 :parent-link l1 :child-link l2 :axis :y :min -100 :max 100)
           j2 (instance rotational-joint :init  :name 'j2
                 :parent-link l2 :child-link l3 :axis :y :min -100 :max 100)
           j3 (instance rotational-joint :init  :name 'j3
                 :parent-link l3 :child-link l4 :axis :y :min -100 :max 100))
     ;;
     (setq links (list l1 l2 l3 l4))
     (setq joint-list (list j1 j2 j3))
     ;;
     (send self :init-ending)
     self))
  (:end-coords (&rest args) (forward-message-to end-coords args))
  )

ここではロボットの手先の座標をend-coordsというスロット変数に格 納し，さらにこれにアクセスするためのメソッドを用意してある．

これまでと同様，

(setq r (instance 3dof-robot :init))
(objects (list r))
(send r :angle-vector #f(30 30 30))

としてロボットモデルの生成，表示，関節角度の指定が可能である． さらに，

(send (send r :end-coords) :draw-on :flush t)

とすると，ロボットのend-coords(端点座標系）の表示が可能であるが， マウスイベントが発生すると消えてしまう．恒久的に表示するためには

(objects (list r (send r :end-coords)))

とするとよい．

次に，ヤコビアン，逆運動学の例を示す．まず基本になるのが，

(send r :link-list (send r :end-coords :parent))

として得られるリンクのリストである．これはロボットのルート（胴体）から 引数となるリンクまでのたどれるリンクを返す．

:calc-jacobian-from-link-listメソッドはリンクのリストを引数にと り，この各リンクに存在するジョイント（関節）に 対応するヤコビアンを計算することができる． また，:move-targetキーワード引数でエンドエフェクタの座標系を 指定してる．その他のキーワード引数については後述する．

(dotimes (i 100)
  (setq j (send r :calc-jacobian-from-link-list
                (send r :link-list (send r :end-coords :parent))
                :move-target (send r :end-coords)
                :rotation-axis t
                :translation-axis t))
  (setq j# (sr-inverse j))
  (setq da (transform j# #f(1 0 0 0 0 0)))
  ;;(setq da (transform j# #f(0 0 0 0 -1 0)))
  (send r :angle-vector (v+ (send r :angle-vector) da))
  (send *irtviewer* :draw-objects)
  )

ここではリンクの長さ（ジョイントの数）は3個なので6行3列のヤコビアン(j)が 計算される．これの逆行列(j#)を作り，位置姿勢の6自由度の目標速度・角速度 (#f(1 0 0 0 0 0))を与えると，それに対応する関節速度(da) が計算でき，これを現在の関節角度に足している ((v+ (send r :angle-vector) da))．

次に，ロボットの端点作業の位置は合わせるが姿勢は拘束せず任意のままでよい，とい う場合の例を示す．ここでは，:calc-jacobian-from-link-listのオプ ショナル引数として:rotation-axis, :translation-axis があり，それぞれ位置，姿勢での拘束条件を示す． tは三軸拘束，nilは拘束なし，その他に:x, :y, :zを指定することができる．

(setq translation-axis t)
(setq rotation-axis nil)
(dotimes (i 2000)
  (setq j (send r :calc-jacobian-from-link-list
                (send r :link-list (send r :end-coords :parent))
                :move-target (send r :end-coords)
                :rotation-axis rotation-axis
                :translation-axis translation-axis))
  (setq j# (sr-inverse j))
  (setq c (make-cascoords :pos (float-vector (* 100 (sin (/ i 500.0))) 0 200)))
  (setq dif-pos (send (send r :end-coords) :difference-position c))
  (setq da (transform j# dif-pos))
  (send r :angle-vector (v+ (send r :angle-vector) da))
  (send *irtviewer* :draw-objects :flush nil)
  (send c :draw-on :flush t)
  )

ここでは位置の三軸のみを拘束した3行3列のヤコビアンを計算し，これの 逆行列からロボットの関節に速度を与えている．さらに，ここでは

(send *irtviewer* :draw-objects :flush nil)

として*irtviewer*に画面を描画しているが，実際に ディスプレイに表示するフラッシュ処理は行わず，その次の行の

(send c :draw-on :flush t)

で目標座標は表示し，かつフラッシュ処理を行っている．

上記の計算をまとめた逆運動学メソッドが:inverse-kinematicsである． 第一引数に目標座標系を指定し，ヤコビアン計算のときと同様にキーワード 引数で :move-target, :translation-axis, :rotation-axis を指定する． また，:debug-viewキーワード引数にtを与えると計算中の様 子をテキスト並びに視覚的に提示してくれる．

(setq c (make-cascoords :pos #f(100 0 0) :rpy (float-vector 0 pi 0)))
(send r :inverse-kinematics  c
      :link-list (send r :link-list (send r :end-coords :parent))
      :move-target (send r :end-coords)
      :translation-axis t
      :rotation-axis t
      :debug-view t)

逆運運動学が失敗する場合のサンプルとして以下のプログラムを見てみよう．

(dotimes (i 400)
  (setq c (make-cascoords
             :pos (float-vector (+ 100 (* 80 (sin (/ i 100.0)))) 0 0)
             :rpy (float-vector 0 pi 0)))
  (send r :inverse-kinematics  c
        :link-list (send r :link-list (send r :end-coords :parent))
        :move-target (send r :end-coords) :translation-axis t  :rotation-axis t)
  (x::window-main-one)
  (send *irtviewer* :draw-objects :flush nil)
  (send c :draw-on :flush t)
  )

このプログラムを実行すると以下のようなエラーが出てくる．

;; inverse-kinematics failed.
;; dif-pos : #f(11.7826 0.0 0.008449)/(11.7826/1)
;; dif-rot : #f(0.0 2.686130e-05 0.0)/(2.686130e-05/0.017453)
;;  coords : #<coordinates #X4bcccb0  0.0 0.0 0.0 / 0.0 0.0 0.0>
;;  angles : (14.9993 150 15.0006)
;;    args : ((#<cascaded-coords #X4b668a0  39.982 0.0 0.0 / 3.142 1.225e-16 3.14
2>) :link-list (#<bodyset-link #X4cf8e60 l2  0.0 0.0 20.0 / 0.0 0.262 0.0> #<body
set-link #X4cc8008 l3  25.866 0.0 116.597 / 3.142 0.262 3.142> #<bodyset-link #X4
c7a0d0 l4  51.764 0.0 20.009 / 3.142 2.686e-05 3.142>) :move-target;; #<cascaded-
coords #X4c93640  51.764 0.0 0.009 / 3.142 2.686e-05 3.142> :translation-axis t :
rotation-axis t)

これは，関節の駆動範囲の制限から目標位置に手先が届かない状況である． このような場面では，例えば，手先の位置さえ目標位置に届けばよく姿勢を 無視してよい場合:rotation-axis nilと指定することができる．

また，:threや:rthreを使うことで逆運動学計算の終了条件で ある位置姿勢の誤差を指定することができる．正確な計算が求められていない 状況ではこの値をデフォルトの1, (deg2rad 1)より大きい値を 利用するのもよい．

また，逆運動学の計算に失敗した場合，デフォルトでは逆運動学計算を始める 前の姿勢まで戻るが，:revert-if-failというキーワード引数をnilと指定 すると，指定されたの回数の計算を繰り替えしたあと，その姿勢のまま関数か ら抜けてくる．指定の回数もまた，:stopというキーワード引数で指 定することができる．

(setq c (make-cascoords :pos #f(300 0 0) :rpy (float-vector 0 pi 0)))
(send r :inverse-kinematics  c
      :link-list (send r :link-list (send r :end-coords :parent))
      :move-target (send r :end-coords)
      :translation-axis t
      :rotation-axis nil
      :revert-if-fail nil)

irteusのサンプルプログラムにおける例

cascaded-coordsクラスでは

  • (:link-list (to &optional form))
  • (:calc-jacobian-from-link-list (link-list &key move-target (rotation-axis nil)))

というメソッドが用意されている．

前者はリンクを引数として，ルートリンクからこのリンクまでの経路を計算し， リンクのリストとして返す．後者はこのリンクのリストを引数とし， move-target座標系をに対するヤコビアンを計算する．

concatenate result-type a bは a bを 連結しresult-type型に変換し返し，scale a b はベクトルbの全ての要素をス カラーa倍し，matrix-logは行列対数関数を計算する．

(if (not (boundp '*irtviewer*)) (make-irtviewer))

(load "irteus/demo/sample-arm-model.l")
(setq *sarm* (instance sarmclass :init))
(send *sarm* :reset-pose)
(setq *target* (make-coords :pos #f(350 200 400)))
(objects (list *sarm* *target*))

(do-until-key
  ;; step 3
  (setq c (send *sarm* :end-coords))
  (send c :draw-on :flush t)
  ;; step 4
  ;; step 4
  (setq dp (scale 0.001 (v- (send *target* :worldpos) (send c :worldpos))) ;; mm->m
        dw (matrix-log (m* (transpose (send c :worldrot)) (send *target* :worldrot))))
  (format t "dp = ~7,3f ~7,3f ~7,3f, dw = ~7,3f ~7,3f ~7,3f~%"
          (elt dp 0) (elt dp 1) (elt dp 2)
          (elt dw 0) (elt dw 1) (elt dw 2))
  ;; step 5
  (when (< (+ (norm dp) (norm dw)) 0.01) (return))
  ;; step 6
  (setq ll (send *sarm* :link-list (send *sarm* :end-coords :parent)))
  (setq j (send *sarm* :calc-jacobian-from-link-list
                ll :move-target (send *sarm* :end-coords)
                :trnaslation-axis t :rotation-axis t))
  (setq q (scale 1.0 (transform (pseudo-inverse j) (concatenate float-vector dp dw))))
  ;; step 7
  (dotimes (i (length ll))
    (send (send (elt ll i) :joint) :joint-angle (elt q i) :relative t))
  ;; draw
  (send *irtviewer* :draw-objects)
  (x::window-main-one))

実際のプログラミングでは:inverse-kinematicsというメソッドが用意されて おり，ここでは特異点や関節リミットの回避，あるいは自己衝突回避等の機能 が追加されている．

実際のロボットモデル

実際のロボットや環境を利用した実践的なサンプルプログラムを見てみよう．

まず，最初はロボットや環境のモデルファイルを読み込む．これらのファイル は$EUSDIR/modelsに，これらのファイルをロードしインスタンスを生成す るプログラムは以下のように書くことができる．(room73b2)や (h7)はこれらのファイル内で定義されている関数である． ロボットのモデル(robot-model)はirtrobot.lファイルで定義 されており，cascaded-linkクラスの子クラスになっている． ロボットとはlarm,rarm,lleg,rleg,headのリンクのツリーからなる ものとして定義されており， (send *robot* :larm)や(send *robot* :head)として ロボットのリム(limb)にアクセスでき，右手の逆運動学，左手の逆運動学等と いう利用方法が可能になっている．

(load "models/room73b2-scene.l")
(load "models/h7-robot.l")
(setq *room* (room73b2))
(setq *robot* (h7))
(objects (list *robot* *room*))

ロボットには:reset-poseというメソッドがありこれで初期姿勢をとる ことができる．

(send *robot* :reset-pose)

次に，ロボットを部屋の中で移動させたい．部屋内の代表的な座標は (send *room* :spots)で取得できる．この中から目的の座標を得る 場合はその座標の名前を引数として:spotメソッドを呼び出す． ちなみに，このメソッドの定義はprog/jskeus/irteus/irtscene.l にあり

(defmethod scene-model
  (:spots
   (&optional name)
   (append
    (mapcan
     #'(lambda(x)(if (derivedp x scene-model) (send x :spots name) nil))
     objs)
    (mapcan #'(lambda (o)
        (if (and (eq (class o) cascaded-coords)
             (or (null name) (string= name (send o :name))))
            (list o)))
        objs)))
  (:spot
   (name)
   (let ((r (send self :spots name)))
     (case (length r)
       (0 (warning-message 1 "could not found spot(~A)" name) nil)
       (1 (car r))
       (t (warning-message 1 "found multiple spot ~A for given name(~A)" r name) (car r)))))
  )

となっている．

ロボットもまたcoordinatesクラスの子クラスなので:move-to メソッドを利用できる．また，このロボットの原点は腰にあるので足が地面に つくように:locateメソッドを使って移動する．

(send *robot* :move-to (send *room* :spot "cook-spot") :world)
(send *robot* :locate #f(0 0 550))

現状では*irtviewer*の画面上でロボットが小さくなっているので， 以下のメソッド利用し，ロボットが画面いっぱいになるように調整する．

(send *irtviewer* :look-all
      (geo::make-bounding-box
       (flatten (send-all (send *robot* :bodies) :vertices))))

次に環境中の物体を選択する．ここでは:objectメソッドを利用する． これは，:spots, :spotと同様の振る舞いをするため， どのような物体があるかは，(send-all (send *room* :objects) :name) として知ることができる． room73b2-kettleの他に room73b2-mug-cupやroom73b2-knife等を利用するとよい．

(setq *kettle* (send *room* :object "room73b2-kettle"))

環境モデルの初期化直後は物体は部屋にassocされているため，以下の用に 親子関係を解消しておく．こうしないと物体を把持するなどの場合に問題が生 じる．

(if (send *kettle* :parent) (send (send *kettle* :parent) :dissoc *kettle*))

ロボットの視線を対象物に向けるためのメソッドとして以下のようなものがあ る．

(send *robot* :head :look-at (send *kettle* :worldpos))

対象物体には，その物体を把持するための利用したらよい座標系が :handleメソッドとして記述されている場合がある．このメソッドは リストを返すため以下の様に(car (send *kettle* :handle))として その座標系を知ることができる．この座標がどこにあるか確認するためには (send (car (send *kettle* :handle)) :draw-on :flush t)とすると よい．

したがってこの物体手を伸ばすためには

(send *robot* :larm :inverse-kinematics
      (car (send *kettle* :handle))
      :link-list (send *robot* :link-list (send *robot* :larm :end-coords :parent))
      :move-target (send *robot* :larm :end-coords)
      :rotation-axis :z
      :debug-view t)

となる．

ここで，ロボットの手先と対象物体の座標系を連結し，

(send *robot* :larm :end-coords :assoc *kettle*)

以下の様にして世界座標系で100[mm]持ち上げることができる．

(send *robot* :larm :move-end-pos #f(0 0 100) :world
        :debug-view t :look-at-target t)

:look-at-targetは移動中に首の向きを常に対象を見つづけるようにす るという指令である．

inverse-kinematicsのtarget-coordsに関数を指定する例

Example of Dual Arm InverseKinematics

Example of Dual Arm InverseKinematics

:inverse-kinematicsの引数target-coordsは``coordinates``クラス以外に coordinatesクラスを返す関数を指定することができる。 以下に示すプログラムは2つの腕を利用してカクテルをふる動作を行うものである()。

(load "irteus/demo/sample-robot-model.l")
(setq *robot* (instance sample-robot :init))
(setq *obj* (make-cylinder 20 100))
(send *obj* :set-color #f(1 1 0))
(send *robot* :reset-pose)
(objects (list *robot* *obj*))

(send *robot* :inverse-kinematics
      (list (make-coords :pos #f(400 0 0)))
      :move-target
      (list (send *robot* :larm :end-coords))
      :link-list
      (list (send *robot* :link-list
                  (send (send *robot* :larm :end-coords) :parent)
                  (car (send *robot* :larm :links))))
      :translation-axis (list t)
      :rotation-axis (list nil))

(let* ((cnt 0.0))
  (do-until-key
   (incf cnt 0.1)
   (send *robot* :inverse-kinematics
         (list (make-coords :pos (float-vector (+ 400 (* 100 (sin cnt))) (* 50 (cos cnt)) 0))
               #'(lambda ()
                   (send (send (send *robot* :larm :end-coords) :copy-worldcoords)
                         :translate #f(0 0 100) :local)))
         :move-target
         (list (send *robot* :larm :end-coords)
               (send *robot* :rarm :end-coords))
         :link-list
         (list (send *robot* :link-list
                     (send (send *robot* :larm :end-coords) :parent)
                     (car (send *robot* :larm :links)))
               (send *robot* :link-list
                     (send (send *robot* :rarm :end-coords) :parent)
                     (car (send *robot* :rarm :links))))
         :translation-axis (list :z t)
         :rotation-axis (list nil :z))
   (send *obj* :newcoords (send (send *robot* :larm :end-coords) :copy-worldcoords))
   (send *irtviewer* :draw-objects)))

(list (make-coords :pos (float-vector (+ 400 (* 100 (sin cnt))) (* 50 (cos cnt)) 0))
      #'(lambda ()
          (send (send (send *robot* :larm :end-coords) :copy-worldcoords)
                :translate #f(0 0 100) :local)))

の行で実際にtarget-coordsに関数を指定している。 この例では、まずカクテルを持つ左手の位置を最初に決める。この時に :translation-axis :z, :rotation-axis nilとなっているため、 z方向の移動量と回転方向は左手の逆運動学の計算に考慮されない。 そして、決まった左手の位置に対して関数が評価されることで 手先のlocal座標から見てz方向に100の位置に対して右手の位置が決まる。 この時、右手の拘束条件は:translation-axis t, :rotation-axis :zとなっ ているためz方向、つまりカクテルの長さ方向を軸としてその軸に対する回転は許した条 件で逆運動学を解くことになる。 このように、拘束条件を踏まえて逆運動学を解きたい場合にはtarget-coordsを関数とし て扱うことが必要になる。

重心位置を考慮したfullbody-inverse-kinematicsの例

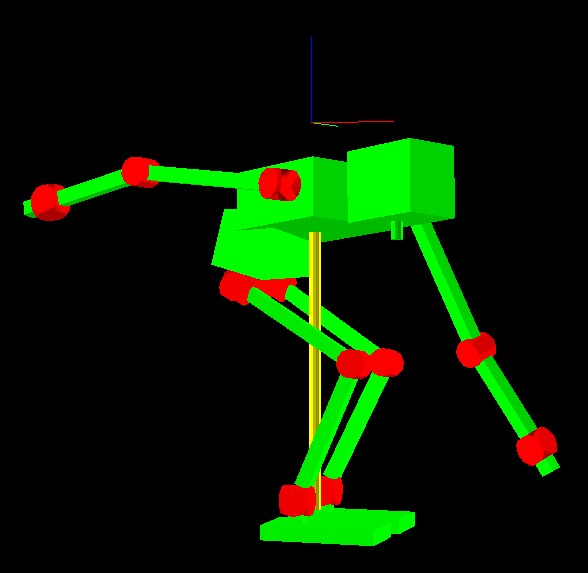
Example of InverseKinematics with root link virtual joint

Example of InverseKinematics with root link virtual joint

:fullbody-inverse-kinematicsはロボットの関節に加えてベースリンク仮想ジョイントを駆動した 逆運動学を解く関数である。以下に示すプログラムは、両足を地面に固定し、重心を両足の上に 位置させた状態で、左手を目標に到達させる動作を行うものである。

(load "irteus/demo/sample-robot-model.l")
(setq *robot* (instance sample-robot :init))
(send *robot* :reset-pose)
(setq *obj* (make-cylinder 10 600))
(send *obj* :rotate pi :x)
(send *obj* :set-color #f(1 1 0))
(objects (list *robot* *obj*))

(let* ((rleg-coords (send *robot* :rleg :end-coords :copy-worldcoords))
       (lleg-coords (send *robot* :lleg :end-coords :copy-worldcoords)))
  (send *robot* :torso :waist-p :joint-angle 10)
  (send *robot* :fullbody-inverse-kinematics
        (list rleg-coords
              lleg-coords
              (make-coords :pos (float-vector 400 100 -600)))
        :move-target
        (list (send *robot* :rleg :end-coords)
              (send *robot* :lleg :end-coords)
              (send *robot* :larm :end-coords))
        :link-list
        (list (send *robot* :link-list (send *robot* :rleg :end-coords :parent))
              (send *robot* :link-list (send *robot* :lleg :end-coords :parent))
              (send *robot* :link-list (send *robot* :larm :end-coords :parent)))
        :translation-axis (list t t t)
        :rotation-axis (list t t nil)
        :target-centroid-pos (midpoint 0.5
                                       (send *robot* :rleg :end-coords :worldpos)
                                       (send *robot* :lleg :end-coords :worldpos))
        :cog-translation-axis :z)
  (send *obj* :locate (send *robot* :centroid) :world)
  (send *irtviewer* :draw-objects))

(list rleg-coords
      lleg-coords
      (make-coords :pos (float-vector 400 100 -600)))

の行でtarget-coordsに右足、左足、左手の目標位置姿勢を指定している。 右足、左足は動かさないため、現在の座標をコピーしたものを与えている。 このときに、:translation-axis (list t t t), :rotation-axis (list t t nil) となっているため、右足、左足は位置姿勢を完全に拘束し、左手は姿勢の 回転は許した条件で逆運動学を解くことになる。

:target-centroid-pos (midpoint 0.5 (send *robot* :rleg :end-coords :worldpos)
                                   (send *robot* :lleg :end-coords :worldpos))
:cog-translation-axis :z)

の行では重心の逆運動学を指定している。:cog-translation-axis :zで z方向の重心の移動は許した状態で、:target-centroid-posで目標重心位置として 両足の中間の座標を与えることによって、重心のxy座標を両足の中間に一致させる 条件のもとで逆運動学を解くことができる。これらの引数は、デフォルト値になっている ので、省略可能である。

外力を考慮したfullbody-inverse-kinematicsを解く例

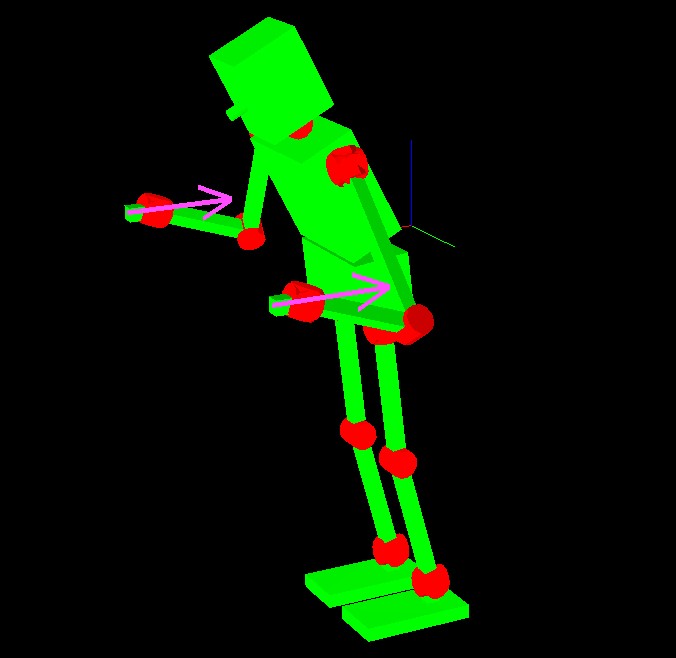
Example of InverseKinematics with external force

Example of InverseKinematics with external force

ロボットが外力、外モーメントを受ける場合、外力による足裏まわりのモーメントと 釣り合うようにロボットの重心をオフセットすることによって、バランスをとることができる。 以下に示すプログラムは両手に外力、外モーメントが加わる場合に、両手両足を目標の位置に 到達させかつバランスが取れる姿勢を逆運動学によって求めるものである。

(load "irteus/demo/sample-robot-model.l")
(setq *robot* (instance sample-robot :init))
(send *robot* :reset-pose)
(setq *obj* (make-cylinder 10 600))
(objects (list *robot*))

(let* ((force-list '(#f(-20 0 0) #f(-20 0 0)))
       (moment-list '(#f(10 0 0) #f(10 0 0))))

  (send *robot* :fullbody-inverse-kinematics
        (list (send *robot* :rleg :end-coords :copy-worldcoords)
              (send *robot* :lleg :end-coords :copy-worldcoords)
              (make-coords :pos #f(400 -300 0))
              (make-coords :pos #f(400 300 0)))
        :move-target (mapcar #'(lambda (x)
                                 (send *robot* x :end-coords))
                             (list :rleg :lleg :rarm :larm))
        :link-list (mapcar #'(lambda (x)
                               (send *robot* :link-list (send *robot* x :end-coords :parent)))
                           (list :rleg :lleg :rarm :larm))
        :centroid-offset-func #'(lambda () (send *robot* :calc-static-balance-point
                                             :force-list force-list
                                             :moment-list moment-list))
        :target-centroid-pos (midpoint 0.5 (send *robot* :rleg :end-coords :worldpos)
                                            (send *robot* :lleg :end-coords :worldpos))
        :cog-translation-axis :z)
  (send *irtviewer* :draw-objects)

  ;; draw force
  (mapcar
   #'(lambda (f cc)
       (let* ((prev-color (send *viewer* :viewsurface :color))
              (prev-width (send *viewer* :viewsurface :line-width)))
         (send *viewer* :viewsurface :color #F(1 0.3 1))
         (send *viewer* :viewsurface :line-width 5)
         (send *irtviewer* :viewer :draw-arrow
               (send cc :worldpos)
               (v+ (send cc :worldpos) (scale 10 f)))
         (send *viewer* :viewsurface :color prev-color)
         (send *viewer* :viewsurface :line-width prev-width)))
   force-list
   (list (send *robot* :rarm :end-coords)
         (send *robot* :larm :end-coords)))
  (send *irtviewer* :viewer :viewsurface :flush)
  )

この例では、

:centroid-offset-func #'(lambda () (send *robot* :calc-static-balance-point
                                     :force-list force-list
                                     :moment-list moment-list))

の行で外力、外モーメントを考慮している。force-listは右手に作用する外力と左手に作用する外力のリスト、force-listは右手に作用する外モーメントと左手に作用する外モーメントのリストであり、単位はそれぞれ[N]、[Nm]である。:calc-static-balance-pointは、現在の両手の位置に作用する外力外モーメントと現在の重心の位置に作用する重力に対して釣り合う足裏圧力中心の位置を返す関数である。:centroid-offset-funcはfloat-vectorクラスを返す関数を指定することができ、現在の重心位置の代わりにこの関数の返り値を用いて目標重心位置との距離を縮める逆運動学を解く。:cog-translation-axis :zでz方向の重心の移動は許した状態で:target-centroid-posで目標重心位置として両足の中間の座標を与えることによって、:centroid-offset-funcの返り値、即ち外力に釣り合いがとれる足裏圧力中心のxy座標を、両足の中間に一致させる逆運動学を解くことができる。

ロボットモデル

ロボットの身体はリンクとジョイントから構成されるが、それぞれ bodyset-linkとjointクラスを利用しモデル絵を作成する。ロ ボットの身体はこれらの要素を含んだcascaded-linkという，連結リン クとしてモデルを生成する．

実際にはjointは抽象クラスであり rotational-joint,linear-joint, wheel-joint,omniwheel-joint, sphere-jointを選択肢、また四肢を持つロボットの場合は cascaded-link ではなくrobot-modelクラスを利用する。

joint

:super = ** propertied-object**
:slots parent-link child-link joint-angle min-angle max-angle default-coords joint-velocity joint-acceleration joint-torque max-joint-velocity max-joint-torque joint-min-max-table joint-min-max-target
:init = `[method]
&key = (name (intern (format nil joint A (system:address self)) KEYWORD)) ((:child-link clink)) ((:parent-link plink)) (min -90) (max 90) ((:max-joint-velocity mjv)) ((:max-joint-torque mjt)) ((:joint-min-max-table mm-table)) ((:joint-min-max-target mm-target)) &allow-other-keys
abstract class of joint, users need to use rotational-joint, linear-joint, sphere-joint, 6dof-joint, wheel-joint or omniwheel-joint.
use :parent-link/:child-link for specifying links that this joint connect to and :min/:min for range of joint angle in degree.

:min-angle &optional v

If v is set, it updates min-angle of this instance. :min-angle returns minimal angle of this joint in degree.

:max-angle &optional v

If v is set, it updates max-angle of this instance. :max-angle returns maximum angle of this joint in degree.

:parent-link &rest args

Returns parent link of this joint. if any arguments is set, it is passed to the parent-link.

:child-link &rest args

Returns child link of this joint. if any arguments is set, it is passed to the child-link.

:joint-dof **

Returns Degree of Freedom of this joint.

:speed-to-angle &rest args

Returns values in deg/mm unit of input value in SI(rad/m) unit.

:angle-to-speed &rest args

Returns values in SI(rad/m) unit of input value in deg/mm unit.

:joint-velocity &optional jv

If jv is set, it updates joint-velocity of this instance. :joint-velocity returns velocity of this joint in SI(m/s, rad/s) unit.

:joint-acceleration &optional ja

If ja is set, it updates joint-acceleration of this instance. :joint-acceleration returns acceleration of this joint in SI(m/\(s^2\), rad/\(s^2\)) unit.

:joint-torque &optional jt

If jt is set, it updates joint-torque of this instance. :joint-torque returns torque of this joint in SI(N, Nm) unit.

:max-joint-velocity &optional mjv

If mjv is set, it updates min-joint-velocity of this instance. :min-joint-velocity returns velocity of this joint in SI(m/s, rad/s) unit.

:max-joint-torque &optional mjt

If mjt is set, it updates min-joint-torque of this instance. :min-joint-torque returns velocity of this joint in SI(N, Nm) unit.

:calc-dav-gain dav i periodic-time

:calc-jacobian &rest args

:joint-min-max-table &optional mm-table

:joint-min-max-target &optional mm-target

:joint-min-max-table-angle-interpolate target-angle min-or-max

:joint-min-max-table-min-angle &optional (target-angle (send joint-min-max-target :joint-angle))

:joint-min-max-table-max-angle &optional (target-angle (send joint-min-max-target :joint-angle))

:max-joint-torque &optional mjt

If mjt is set, it updates min-joint-torque of this instance. :min-joint-torque returns velocity of this joint in SI(N, Nm) unit.

:max-joint-velocity &optional mjv

If mjv is set, it updates min-joint-velocity of this instance. :min-joint-velocity returns velocity of this joint in SI(m/s, rad/s) unit.

:joint-torque &optional jt

If jt is set, it updates joint-torque of this instance. :joint-torque returns torque of this joint in SI(N, Nm) unit.

:joint-acceleration &optional ja

If ja is set, it updates joint-acceleration of this instance. :joint-acceleration returns acceleration of this joint in SI(m/\(s^2\), rad/\(s^2\)) unit.

:joint-velocity &optional jv

If jv is set, it updates joint-velocity of this instance. :joint-velocity returns velocity of this joint in SI(m/s, rad/s) unit.

:angle-to-speed &rest args

Returns values in SI(rad/m) unit of input value in deg/mm unit.

:speed-to-angle &rest args

Returns values in deg/mm unit of input value in SI(rad/m) unit.

:joint-dof **

Returns Degree of Freedom of this joint.

:child-link &rest args

Returns child link of this joint. if any arguments is set, it is passed to the child-link.

:parent-link &rest args

Returns parent link of this joint. if any arguments is set, it is passed to the parent-link.

:max-angle &optional v

If v is set, it updates max-angle of this instance. :max-angle returns maximum angle of this joint in degree.

:min-angle &optional v

If v is set, it updates min-angle of this instance. :min-angle returns minimal angle of this joint in degree.

:init = `[method]
&key = (name (intern (format nil joint A (system:address self)) KEYWORD)) ((:child-link clink)) ((:parent-link plink)) (min -90) (max 90) ((:max-joint-velocity mjv)) ((:max-joint-torque mjt)) ((:joint-min-max-table mm-table)) ((:joint-min-max-target mm-target)) &allow-other-keys
abstract class of joint, users need to use rotational-joint, linear-joint, sphere-joint, 6dof-joint, wheel-joint or omniwheel-joint.
use :parent-link/:child-link for specifying links that this joint connect to and :min/:min for range of joint angle in degree.

:joint-min-max-table-max-angle &optional (target-angle (send joint-min-max-target :joint-angle))

:joint-min-max-table-min-angle &optional (target-angle (send joint-min-max-target :joint-angle))

:joint-min-max-table-angle-interpolate target-angle min-or-max

:joint-min-max-target &optional mm-target

:joint-min-max-table &optional mm-table

:calc-jacobian &rest args

:calc-dav-gain dav i periodic-time

rotational-joint

:super = ** joint**
:slots axis
:init = `[method]
&rest args &key = ((:axis ax) :z) ((:max-joint-velocity mjv) 5) ((:max-joint-torque mjt) 100) &allow-other-keys

create instance of rotational-joint. :axis is either (:x, :y, :z) or vector. :min-angle and :max-angle takes in radius, but velocity and torque are given in SI units.

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys

Return joint-angle if v is not set, if v is given, set joint angle. v is rotational value in degree.

:joint-dof **

Returns DOF of rotational joint, 1.

:speed-to-angle v

Returns degree of given input in radian

:angle-to-speed v

Returns radian of given input in degree

:calc-angle-speed-gain dav i periodic-time

:calc-jacobian &rest args

:angle-to-speed v

Returns radian of given input in degree

:speed-to-angle v

Returns degree of given input in radian

:joint-dof **

Returns DOF of rotational joint, 1.

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys

Return joint-angle if v is not set, if v is given, set joint angle. v is rotational value in degree.

:init = `[method]
&rest args &key = ((:axis ax) :z) ((:max-joint-velocity mjv) 5) ((:max-joint-torque mjt) 100) &allow-other-keys

create instance of rotational-joint. :axis is either (:x, :y, :z) or vector. :min-angle and :max-angle takes in radius, but velocity and torque are given in SI units.

:calc-jacobian &rest args

:calc-angle-speed-gain dav i periodic-time

linear-joint

:super = ** joint**
:slots axis
:init = `[method]
&rest args &key = ((:axis ax) :z) ((:max-joint-velocity mjv) (/ pi 4)) ((:max-joint-torque mjt) 100) &allow-other-keys

Create instance of linear-joint. :axis is either (:x, :y, :z) or vector. :min-angle and :max-angle takes in [mm], but velocity and torque are given in SI units.

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys

return joint-angle if v is not set, if v is given, set joint angle. v is linear value in [mm].

:joint-dof **

Returns DOF of linear joint, 1.

:speed-to-angle v

Returns [mm] of given input in [m]

:angle-to-speed v

Returns [m] of given input in [mm]

:calc-angle-speed-gain dav i periodic-time

:calc-jacobian &rest args

:angle-to-speed v

Returns [m] of given input in [mm]

:speed-to-angle v

Returns [mm] of given input in [m]

:joint-dof **

Returns DOF of linear joint, 1.

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys

return joint-angle if v is not set, if v is given, set joint angle. v is linear value in [mm].

:init = `[method]
&rest args &key = ((:axis ax) :z) ((:max-joint-velocity mjv) (/ pi 4)) ((:max-joint-torque mjt) 100) &allow-other-keys

Create instance of linear-joint. :axis is either (:x, :y, :z) or vector. :min-angle and :max-angle takes in [mm], but velocity and torque are given in SI units.

:calc-jacobian &rest args

:calc-angle-speed-gain dav i periodic-time

wheel-joint

:super = ** joint**
:slots axis
:init = `[method]
&rest args &key = (min (float-vector -inf-inf)) (max (float-vector infinf)) ((:max-joint-velocity mjv) (float-vector (/ 0.08 0.05) (/ pi 4))) ((:max-joint-torque mjt) (float-vector 100 100)) &allow-other-keys

Create instance of wheel-joint.

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys

return joint-angle if v is not set, if v is given, set joint angle. v is joint-angle vector, which is (float-vector translation-x[mm] rotation-z[deg])

:joint-dof **

Returns DOF of linear joint, 2.

:speed-to-angle dv

Returns [mm/deg] of given input in SI unit [m/rad]

:angle-to-speed dv

Returns SI unit [m/rad] of given input in [mm/deg]

:calc-angle-speed-gain dav i periodic-time

:calc-jacobian fik row column joint paxis child-link world-default-coords child-reverse move-target transform-coords rotation-axis translation-axis tmp-v0 tmp-v1 tmp-v2 tmp-v3 tmp-v3a tmp-v3b tmp-m33

:angle-to-speed dv

Returns SI unit [m/rad] of given input in [mm/deg]

:speed-to-angle dv

Returns [mm/deg] of given input in SI unit [m/rad]

:joint-dof **

Returns DOF of linear joint, 2.

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys

return joint-angle if v is not set, if v is given, set joint angle. v is joint-angle vector, which is (float-vector translation-x[mm] rotation-z[deg])

:init = `[method]
&rest args &key = (min (float-vector -inf-inf)) (max (float-vector infinf)) ((:max-joint-velocity mjv) (float-vector (/ 0.08 0.05) (/ pi 4))) ((:max-joint-torque mjt) (float-vector 100 100)) &allow-other-keys

Create instance of wheel-joint.

:calc-jacobian fik row column joint paxis child-link world-default-coords child-reverse move-target transform-coords rotation-axis translation-axis tmp-v0 tmp-v1 tmp-v2 tmp-v3 tmp-v3a tmp-v3b tmp-m33

:calc-angle-speed-gain dav i periodic-time

omniwheel-joint

:super = ** joint**
:slots axis
:init = `[method]
&rest args &key = (min (float-vector -inf-inf-inf)) (max (float-vector infinfinf)) ((:max-joint-velocity mjv) (float-vector (/ 0.08 0.05) (/ 0.08 0.05) (/ pi 4))) ((:max-joint-torque mjt) (float-vector 100 100 100)) &allow-other-keys

create instance of omniwheel-joint.

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys

return joint-angle if v is not set, if v is given, set joint angle. v is joint-angle vector, which is (float-vector translation-x[mm] translation-y[mm] rotation-z[deg])

:joint-dof **

Returns DOF of linear joint, 3.

:speed-to-angle dv

Returns [mm/deg] of given input in SI unit [m/rad]

:angle-to-speed dv

Returns SI unit [m/rad] of given input in [mm/deg]

:calc-angle-speed-gain dav i periodic-time

:calc-jacobian fik row column joint paxis child-link world-default-coords child-reverse move-target transform-coords rotation-axis translation-axis tmp-v0 tmp-v1 tmp-v2 tmp-v3 tmp-v3a tmp-v3b tmp-m33

:angle-to-speed dv

Returns SI unit [m/rad] of given input in [mm/deg]

:speed-to-angle dv

Returns [mm/deg] of given input in SI unit [m/rad]

:joint-dof **

Returns DOF of linear joint, 3.

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys

return joint-angle if v is not set, if v is given, set joint angle. v is joint-angle vector, which is (float-vector translation-x[mm] translation-y[mm] rotation-z[deg])

:init = `[method]
&rest args &key = (min (float-vector -inf-inf-inf)) (max (float-vector infinfinf)) ((:max-joint-velocity mjv) (float-vector (/ 0.08 0.05) (/ 0.08 0.05) (/ pi 4))) ((:max-joint-torque mjt) (float-vector 100 100 100)) &allow-other-keys

create instance of omniwheel-joint.

:calc-jacobian fik row column joint paxis child-link world-default-coords child-reverse move-target transform-coords rotation-axis translation-axis tmp-v0 tmp-v1 tmp-v2 tmp-v3 tmp-v3a tmp-v3b tmp-m33

:calc-angle-speed-gain dav i periodic-time

sphere-joint

:super = ** joint**
:slots axis
:init = `[method]
&rest args &key = (min (float-vector -inf-inf-inf)) (max (float-vector infinfinf)) ((:max-joint-velocity mjv) (float-vector (/ pi 4) (/ pi 4) (/ pi 4))) ((:max-joint-torque mjt) (float-vector 100 100 100)) &allow-other-keys

Create instance of sphere-joint. min/max are defind as a region of angular velocity in degree.

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys
return joint-angle if v is not set, if v is given, set joint angle.
v is joint-angle vector [deg] by axis-angle representation, i.e (scale rotation-angle-from-default-coords[deg] axis-unit-vector)

:joint-angle-rpy &optional v &key relative

Return joint-angle if v is not set, if v is given, set joint-angle vector by RPY representation, i.e. (float-vector yaw[deg] roll[deg] pitch[deg])

:joint-dof **

Returns DOF of linear joint, 3.

:speed-to-angle dv

Returns degree of given input in radian

:angle-to-speed dv

Returns radian of given input in degree

:joint-euler-angle = `[method]
&key = (axis-order ’(:z :y :x)) ((:child-rot m) (send child-link :rot))

Return joint-angle if v is not set, if v is given, set joint-angle vector by euler representation.

:calc-angle-speed-gain dav i periodic-time

:calc-jacobian fik row column joint paxis child-link world-default-coords child-reverse move-target transform-coords rotation-axis translation-axis tmp-v0 tmp-v1 tmp-v2 tmp-v3 tmp-v3a tmp-v3b tmp-m33

:joint-euler-angle = `[method]
&key = (axis-order ’(:z :y :x)) ((:child-rot m) (send child-link :rot))

Return joint-angle if v is not set, if v is given, set joint-angle vector by euler representation.

:angle-to-speed dv

Returns radian of given input in degree

:speed-to-angle dv

Returns degree of given input in radian

:joint-dof **

Returns DOF of linear joint, 3.

:joint-angle-rpy &optional v &key relative

Return joint-angle if v is not set, if v is given, set joint-angle vector by RPY representation, i.e. (float-vector yaw[deg] roll[deg] pitch[deg])

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys
return joint-angle if v is not set, if v is given, set joint angle.
v is joint-angle vector [deg] by axis-angle representation, i.e (scale rotation-angle-from-default-coords[deg] axis-unit-vector)
:init = `[method]
&rest args &key = (min (float-vector -inf-inf-inf)) (max (float-vector infinfinf)) ((:max-joint-velocity mjv) (float-vector (/ pi 4) (/ pi 4) (/ pi 4))) ((:max-joint-torque mjt) (float-vector 100 100 100)) &allow-other-keys

Create instance of sphere-joint. min/max are defind as a region of angular velocity in degree.

:calc-jacobian fik row column joint paxis child-link world-default-coords child-reverse move-target transform-coords rotation-axis translation-axis tmp-v0 tmp-v1 tmp-v2 tmp-v3 tmp-v3a tmp-v3b tmp-m33

:calc-angle-speed-gain dav i periodic-time

6dof-joint

:super = ** joint**
:slots axis
:init = `[method]
&rest args &key = (min (float-vector -inf-inf-inf-inf-inf-inf)) (max (float-vector infinfinfinfinfinf)) ((:max-joint-velocity mjv) (float-vector (/ 0.08 0.05) (/ 0.08 0.05) (/ 0.08 0.05) (/ pi 4) (/ pi 4) (/ pi 4))) ((:max-joint-mjt mjt) (float-vector 100 100 100 100 100 100)) (absolute-p nil) &allow-other-keys

Create instance of 6dof-joint.

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys

Return joint-angle if v is not set, if v is given, set joint angle vector, which is 6D vector of 3D translation[mm] and 3D rotation[deg], i.e. (find-if #’(lambda (x) (eq (send (car x) :name) ’sphere-joint)) (documentation :joint-angle))

:joint-angle-rpy &optional v &key relative

Return joint-angle if v is not set, if v is given, set joint angle. v is joint-angle vector, which is 6D vector of 3D translation[mm] and 3D rotation[deg], for rotation, please see (find-if #’(lambda (x) (eq (send (car x) :name) ’sphere-joint)) (documentation :joint-angle-rpy))

:joint-dof **

Returns DOF of linear joint, 6.

:speed-to-angle dv

Returns [mm/deg] of given input in SI unit [m/rad]

:angle-to-speed dv

Returns SI unit [m/rad] of given input in [mm/deg]

:calc-angle-speed-gain dav i periodic-time

:calc-jacobian fik row column joint paxis child-link world-default-coords child-reverse move-target transform-coords rotation-axis translation-axis tmp-v0 tmp-v1 tmp-v2 tmp-v3 tmp-v3a tmp-v3b tmp-m33

:angle-to-speed dv

Returns SI unit [m/rad] of given input in [mm/deg]

:speed-to-angle dv

Returns [mm/deg] of given input in SI unit [m/rad]

:joint-dof **

Returns DOF of linear joint, 6.

:joint-angle-rpy &optional v &key relative

Return joint-angle if v is not set, if v is given, set joint angle. v is joint-angle vector, which is 6D vector of 3D translation[mm] and 3D rotation[deg], for rotation, please see (find-if #’(lambda (x) (eq (send (car x) :name) ’sphere-joint)) (documentation :joint-angle-rpy))

:joint-angle = `[method]
&optional v &key = relative &allow-other-keys

Return joint-angle if v is not set, if v is given, set joint angle vector, which is 6D vector of 3D translation[mm] and 3D rotation[deg], i.e. (find-if #’(lambda (x) (eq (send (car x) :name) ’sphere-joint)) (documentation :joint-angle))

:init = `[method]
&rest args &key = (min (float-vector -inf-inf-inf-inf-inf-inf)) (max (float-vector infinfinfinfinfinf)) ((:max-joint-velocity mjv) (float-vector (/ 0.08 0.05) (/ 0.08 0.05) (/ 0.08 0.05) (/ pi 4) (/ pi 4) (/ pi 4))) ((:max-joint-mjt mjt) (float-vector 100 100 100 100 100 100)) (absolute-p nil) &allow-other-keys

Create instance of 6dof-joint.

:calc-jacobian fik row column joint paxis child-link world-default-coords child-reverse move-target transform-coords rotation-axis translation-axis tmp-v0 tmp-v1 tmp-v2 tmp-v3 tmp-v3a tmp-v3b tmp-m33

:calc-angle-speed-gain dav i periodic-time

bodyset-link

:super = ** bodyset**
:slots joint parent-link child-links analysis-level default-coords weight acentroid inertia-tensor angular-velocity angular-acceleration spacial-velocity spacial-acceleration momentum-velocity angular-momentum-velocity momentum angular-momentum force moment ext-force ext-moment
:init = `[method]
coords &rest args &key = ((:analysis-level level) :body) ((:weight w) 1) ((:centroid c) #f(0.0 0.0 0.0)) ((:inertia-tensor i) (unit-matrix 3)) &allow-other-keys

Create instance of bodyset-link.

:worldcoords &optional (level analysis-level)

Returns a coordinates object which represents this coord in the world by concatenating all the cascoords from the root to this coords.

:analysis-level &optional v

Change analysis level :coords only changes kinematics level and :body changes geometry too.

:weight &optional w

Returns a weight of the link. If w is given, set weight.

:centroid &optional c

Returns a centroid of the link. If c is given, set new centroid.

:inertia-tensor &optional i

Returns a inertia tensor of the link. If c is given, set new intertia tensor.

:joint &rest args

Returns a joint associated with this link. If args is given, args are forward to the joint.

:add-joint j

Set j as joint of this link

:del-joint **

Remove current joint of this link

:parent-link **

Returns parent link

:child-links **

Returns child links

:add-child-links l

Add l to child links

:add-parent-link l

Set l as parent link

:del-child-link l

Delete l from child links

:del-parent-link **

Delete parent link

:default-coords &optional c

:del-parent-link **

Delete parent link

:del-child-link l

Delete l from child links

:add-parent-link l

Set l as parent link

:add-child-links l

Add l to child links

:child-links **

Returns child links

:parent-link **

Returns parent link

:del-joint **

Remove current joint of this link

:add-joint j

Set j as joint of this link

:joint &rest args

Returns a joint associated with this link. If args is given, args are forward to the joint.

:inertia-tensor &optional i

Returns a inertia tensor of the link. If c is given, set new intertia tensor.

:centroid &optional c

Returns a centroid of the link. If c is given, set new centroid.

:weight &optional w

Returns a weight of the link. If w is given, set weight.

:analysis-level &optional v

Change analysis level :coords only changes kinematics level and :body changes geometry too.

:worldcoords &optional (level analysis-level)

Returns a coordinates object which represents this coord in the world by concatenating all the cascoords from the root to this coords.

:init = `[method]
coords &rest args &key = ((:analysis-level level) :body) ((:weight w) 1) ((:centroid c) #f(0.0 0.0 0.0)) ((:inertia-tensor i) (unit-matrix 3)) &allow-other-keys

Create instance of bodyset-link.

:default-coords &optional c

cascaded-link

:super = ** cascaded-coords**
:slots links joint-list bodies collision-avoidance-links end-coords-list
:init = `[method]
&rest args &key = name &allow-other-keys

Create cascaded-link.

:init-ending **

This method is to called finalize the instantiation of the cascaded-link. This update bodies and child-link and parent link from joint-list

:links &rest args

Returns links, or args is passed to links

:joint-list &rest args

Returns joint list, or args is passed to joints

:link name

Return a link with given name.

:joint name

Return a joint with given name.

:end-coords name

Returns end-coords with given name

:bodies &rest args

Return bodies of this object. If args is given it passed to all bodies

:faces **

Return faces of this object.

:angle-vector &optional vec (angle-vector (instantiate float-vector (calc-target-joint-dimension joint-list)))

Returns angle-vector of this object, if vec is given, it updates angles of all joint. If given angle-vector violate min/max range, the value is modified.

:link-list to &optional from

Find link list from to link to from link.

:plot-joint-min-max-table joint0 joint1

Plot joint min max table on Euslisp window.

:calc-jacobian-from-link-list = `[method]
link-list &rest args &key = move-target (transform-coords move-target) (rotation-axis (cond ((atom move-target) nil) (t (make-list (length move-target))))) (translation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t)))) (col-offset 0) (dim (send self :calc-target-axis-dimension rotation-axis translation-axis)) (fik-len (send self :calc-target-joint-dimension link-list)) fik (tmp-v0 (instantiate float-vector 0)) (tmp-v1 (instantiate float-vector 1)) (tmp-v2 (instantiate float-vector 2)) (tmp-v3 (instantiate float-vector 3)) (tmp-v3a (instantiate float-vector 3)) (tmp-v3b (instantiate float-vector 3)) (tmp-m33 (make-matrix 3 3)) &allow-other-keys
Calculate jacobian matrix from link-list and move-target. Jacobian is represented in :transform-coords. Unit system is [m] or [rad], not [mm] or [deg].
Joint order for this jacobian matrix follows link-list order. Joint torque[Nm] order is also the same.
Ex1. One-Arm
(setq rarm-link-list(send robot:link-list (send robot:rarm :end-coords :parent)))
(send-all rarm-link-list:joint)
Ex2. Two-Arm
(setq arms-link-list(mapcar #’(lambda (l) (send robot:link-list (send robotl :end-coords :parent))) ’(:rarm :larm)))
(send-all (send robot:calc-union-link-list arms-link-list) :joint)
:move-joints-avoidance = `[method]
union-vel &rest args &key = union-link-list link-list (fik-len (send self :calc-target-joint-dimension union-link-list)) (weight (fill (instantiate float-vector fik-len) 1)) (null-space) (avoid-nspace-gain 0.01) (avoid-weight-gain 1.0) (avoid-collision-distance 200) (avoid-collision-null-gain 1.0) (avoid-collision-joint-gain 1.0) ((:collision-avoidance-link-pair pair-list) (send self :collision-avoidance-link-pair-from-link-list link-list :obstacles (cadr (memq :obstacles args)) :debug (cadr (memq :debug-view args)))) (cog-gain 0.0) (target-centroid-pos) (centroid-offset-func) (cog-translation-axis :z) (cog-null-space nil) (additional-weight-list) (additional-nspace-list) (tmp-len (instantiate float-vector fik-len)) (tmp-len2 (instantiate float-vector fik-len)) (tmp-weight (instantiate float-vector fik-len)) (tmp-nspace (instantiate float-vector fik-len)) (tmp-mcc (make-matrix fik-len fik-len)) (tmp-mcc2 (make-matrix fik-len fik-len)) (debug-view) (jacobi) &allow-other-keys
:move-joints-avoidance is called in :inverse-kinematics-loop. In this method, calculation of joint position difference are executed and joint positon are moved.
Optional arguments:
  :weight
   float-vector of inverse weight of velocity of each joint or a function which returns the float-vector or a list which returns the float-vector. Length of the float-vector should be same as the number of columns of the jacobian. If :weight is a function or a list, it is called in each IK loop as (funcall weight union-link-list) or (eval weight). :weight is used in calculation of weighted norm of joint velocity for sr-inverse. Default is the float-vector filled with 1.
  :null-space
   float-vector of joint velocity or a function which returns the float-vector or a list which returns the float-vector. Length of the float-vector should be same as the number of columns of the jacobian. If :null-space is a function or a list, it is called in each IK loop as (funcall null-space) or (eval null-space). This joint velocity is applied in null space of main task in each IK loop. Default is nil.
  :avoid-nspace-gain
  gain of joint velocity to avoid joint limit applied in null space of main task in each IK loop. The avoiding velocity is calculated as \((((t\_max + t\_min)/2 - t) / ((t\_max - t\_min)/2))^2\). Default is 0.01.
  :avoid-weight-gain
   gain of dH/dt in calcuration of avoiding joint limits weight. :weight is devided by this avoiding joint limits weight. Default is 1.0.
   If :avoid-nspace-gain is 0, :weight is multipled by :weight instead.
  :avoid-collision-distance
   yellow zone. 0.1avoid-collision-distance is regarded as orange zone.
   If :avoid-collision-joint-gain is smaller than or equal to 0.0, yellow zone and orange zone become inactive. Default is 200[mm].
  :avoid-collision-null-gain
   \(k\_{null}\). Default is 1.0.
  :avoid-collision-joint-gain
   \(k\_{joint}\). Default is 1.0.
  :collision-avoidance-link-pair
   (list (list link1 link2) (list link3 link4) ...) with any length. Collision between paired links is cared. Default is (send self :collision-avoidance-link-pair-from-link-list link-list :obstacles (cadr (memq :obstacles args))).
  :additional-weight-list
   (list (list target-link1 additional-weight1) (list target-link2 additional-weight2) ...) with any length. The component of :weight corresponding to the parent joint of target-link is scaled by additional-weight. additional-weight should be float (if 1 dof), float-vector with length of the joint dof, or a function which returns the float or float-vector. if additional-weight is a function, it is called in each IK loop as (funcall additional-weight). Default is nil.
  :additional-nspace-list
   (list (list target-link1 var1) (list target-link2 var2) ...) with any length. In each IK loop, the parent joint of target-link is moved by the amount of var in null space of main task. var should be float (if 1dof), float-vector with the same length of the target joint dof, or a function which returns the float or float-vector.If var is float-vector, it is called in each IK loop as (funcall var). Default is nil.
  other-keys
   :manipulability-limit
    If manipulability of jacobian is smaller than manipulability-limit, diagonal matrix is added in calculation of sr-inverse. Default is 0.1.
  :manipulability-gain
   Weight of diagonal matrix in calculation of sr-inverse. Weight is calculated as (manipulability-gain (expt (- 1.0 (/ manipulability manipulability-limit)) 2)). Default is 0.001.
   :collision-distance-limit
    Threshold for collision detection. If collision is detected, the distance between the colliding links is considered to be :collision-distance-limit instead of actual distance. Default is 10[mm].
   :move-joints-hook
    A function which is called right after joints are moved in each IK loop as (funcall move-joints-hook). Default is nil.
:inverse-kinematics-loop = `[method]
dif-pos dif-rot &rest args &key = (stop 1) (loop 0) link-list move-target (rotation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t)))) (translation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t)))) (thre (cond ((atom move-target) 1) (t (make-list (length move-target) :initial-element 1)))) (rthre (cond ((atom move-target) (deg2rad 1)) (t (make-list (length move-target) :initial-element (deg2rad 1))))) (dif-pos-ratio 1.0) (dif-rot-ratio 1.0) union-link-list target-coords (jacobi) (additional-check) (additional-jacobi) (additional-vel) (centroid-thre 1.0) (target-centroid-pos) (centroid-offset-func) (cog-translation-axis :z) (cog-null-space nil) (cog-gain 1.0) (min-loop (/ stop 10)) debug-view ik-args &allow-other-keys
:inverse-kinematics-loop is one loop calculation for :inverse-kinematics.
In this method, joint position difference satisfying workspace difference (dif-pos, dif-rot) are calculated and euslisp model joint angles are updated.
Optional arguments:
  :dif-pos-ratio
   Ratio of spacial velocity used in calculation of joint position difference to workspace difference (after :p-limit applied). Default is 1.0.
  :dif-rot-ratio
   Ratio of angular velocity used in calculation of joint position difference to workspace difference (after :r-limit applied). Default is 1.0.
  :jacobi
   A jacobian of all move-target or a function that returns the jacobian. When a function is given, It is called in every IK loop as (funcall jacobi link-list move-target translation-axis rotation-axis). Default is (sendself :calc-jacobian-from-link-list link-list :translation-axis translation-axis :rotation-axis rotation-axis :move-target move-target method-args).
  :additional-check
   This argument is to add optional best-effort convergence conditions. Default is nil (no additional check). :additional-check should be function or lambda.
   best-effort =>
    In :inverse-kinematics-loop, ’success’ is overwritten by ’(and success additional-check)’
    In :inverse-kinematics, ’success is not overwritten.
    So, :inverse-kinematics-loop wait until ’:additional-check’ becomes ’t’ as possible,
    but ’:additional-check’ is neglected in the final :inverse-kinematics return.
  :cog-gain
   Ratio of centroid velocity used in calculation of joint position difference to centroid position difference. max 1.0. Default is 1.0.
  :min-loop
   Minimam loop count. Defalt (/ stop 10).
   If integer is specified, :inverse-kinematics-loop does returns :ik-continues and continuing solving IK.
   If min-loop is nil, do not consider loop counting for IK convergence.
  other-keys
   :move-joints-avoidance is internally called and args are passed to it. See the explanation of :move-joints-avoidance.
   :p-limit
    Maximum spacial velocity of each move-target in one IK loop. Default is 100.0[mm].
   :r-limit
    Maximum angular velocity of each move-target in one IK loop. Default is 0.5[rad].
:inverse-kinematics = `[method]
target-coords &rest args &key = (stop 50) (link-list) (move-target) (debug-view) (warnp t) (revert-if-fail t) (rotation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t)))) (translation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t)))) (joint-args) (thre (cond ((atom move-target) 1) (t (make-list (length move-target) :initial-element 1)))) (rthre (cond ((atom move-target) (deg2rad 1)) (t (make-list (length move-target) :initial-element (deg2rad 1))))) (union-link-list) (centroid-thre 1.0) (target-centroid-pos) (centroid-offset-func) (cog-translation-axis :z) (cog-null-space nil) (dump-command :fail-only) (periodic-time 0.5) (check-collision) (additional-jacobi) (additional-vel) &allow-other-keys
Move move-target to target-coords.
;; target-coords, link-list and move-target need to be given.
;; target-coords, move-target, rotation-axis, translation-axis, link-list
;; ->both list and atom OK.
:target-coords
  The coordinate of the target, or a function that returns coordinates. When a function is given, it is called in every IK loop as (funcall target-coords). Use a list of targets to solve the IK relative to multiple end links simultaneously.
:stop
  Maximum number for IK iteration. Default is 50.
:link-list
  List of links to control. When the target-coords is list, this should be a list of lists.
:move-target
  Specify end-effector coordinate. When the target-coords is list, this should be list too.
:debug-view
  Set t to show debug message and visualization. Use :no-message to just show the irtview image. Default is nil.
:warnp
  Set nil to not display debug message when the IK failed. Default is t.
:revert-if-fail
  Set nil to keep the angle posture of IK solve iteration. Default is t, which return to original position when IK fails.
:rotation-axis
  Use nil for position only IK. :x, :y, :z for the constraint around axis with plus direction, :-x :-y :-z for axis with minus direction. :zz :yy :zz for direction free axis. :xm :ym :zm for allowing rotation with respect to mirror direction. When the target-coords is list, this should be list too. Default is t.
:translation-axis
  :x :y :z for constraint along the x, y, z axis. :xy :yz :zx for plane. Default is t.
:joint-args
  Arguments passed to joint as (sendjoint :joint-angle angle :relative t joint-args). Default nil.
:thre
  Threshold for position error to terminate IK iteration. Default is 1 [mm].
:rthre
  Threshold for rotation error to terminate IK iteration. Default is 0.017453 [rad] (1 deg).
:union-link-list
  a function that returns union of link-list called as (funcall union-link-list link-list). Default is (send self :calc-union-link-list link-list).
:centroid-thre
  Threshold for centroid position error to terminate IK iteration. Default is 1 [mm].
:target-centroid-pos
  The float-vector of the target centroid position. Default is nil.
:centroid-offset-func
  A function that returns centroid position. This function is called in each IK loop as (funcall centroid-offset-func). Default is (send self :centroid).
:cog-translation-axis
  :x :y :z for constraint along the x, y, z axis. :xy :yz :zx for plane. t for point. Default is :z.
:cog-null-space
  t: centroid position task is solved in null space of the main task. Default is nil.
:dump-command
 should be t, nil, :always, :fail-only, :always-with-debug-log, or :fail-only-with-debug-log. Log are success/fail log and ik debug information log.
   t or :always : dump log both in success and fail (for success/fail log).
   :always-with-debug-log : dump log both in success and fail (for success/fail log and ik debug information log).
   :fail-only : dump log only in fail (for success/fail log).
   :always-with-debug-log : dump log only in fail (for success/fail log and ik debug information log).
   nil : do not dump log.
:periodic-time
  The amount of joint angle modification in each IK loop is scaled not to violate joint velocity limit times :periodic-time. Default is 0.5[s].
:check-collision
  Set t to return false when self collision occurs at found IK solution. Default is nil. To avoid collision within IK loop, use set links to collision-avoidance-links slot of cascaded-link.
:additional-jacobi
  The jacobian of the additional main task, or a function that returns the jacobian. When a function is given, it is called in every IK loop as (funcall additional-jacobi link-list). Use a list of additional-jacobi to solve the IK for multiple additional task. Default is nil.
:additional-vel
  The velocity of additional main task, or a function that returns the velocity. When a function is given, it is called in every IK loop as (funcall additional-vel link-list). The velocity should be expressed in the same coordinates as corresponding additional-jacobi. When the additional-jacobi is list, this should be a list of same length. Default is nil.
other-keys
  function :inverse-kinematics-loop is internally called and args are passed to it. See the explanation of :inverse-kinematics-loop.
:calc-grasp-matrix = `[method]
contact-points &key = (ret (make-matrix 6 (6 (length contact-points)))) (contact-rots (mapcar #’(lambda (r) (unit-matrix 3)) contact-points))
Calc grasp matrix.
Grasp matrix is defined as
| E_3 0 E_3 0 ... |
| p1x E_3 p2x E_3 ... |
Arguments:
contact-points is list of contact points[mm].
contact-rots is list of contact coords rotation[rad].
If contact-rots is specified, grasp matrix as follow:
| R1 0 R2 0 ... |
| p1xR1 R1 p2xR2 R2 ... |
:inverse-kinematics-for-closed-loop-forward-kinematics = `[method]
target-coords &rest args &key = (move-target) (link-list) (move-joints-hook) (additional-weight-list) (constrained-joint-list) (constrained-joint-angle-list) (min-loop 2) &allow-other-keys
Solve inverse-kinematics for closed loop forward kinematics.
Move move-target to target-coords with link-list.
link-list loop should be close when move-target reaches target-coords.
constrained-joint-list is list of joints specified given joint angles in closed loop.
constrained-joint-angle-list is list of joint-angle for constrained-joint-list.

:calc-jacobian-for-interlocking-joints link-list &key (interlocking-joint-pairs (send self :interlocking-joint-pairs))

Calculate jacobian to keep interlocking joint velocity same.
dtheta_0 = dtheta_1 =>[... 0 1 0 ... 0 -1 0 .... ][...dtheta_0...dtheta_1...]

:calc-vel-for-interlocking-joints link-list &key (interlocking-joint-pairs (send self :interlocking-joint-pairs))

Calculate 0 velocity for keeping interlocking joint at the same joint angle.

:set-midpoint-for-interlocking-joints &key (interlocking-joint-pairs (send self :interlocking-joint-pairs))

Set interlocking joints at mid point of each joint angle.

:interlocking-joint-pairs **

Interlocking joint pairs.
pairs are (list (cons joint0 joint1) ... )
If users want to use interlocking joints, please overwrite this method.
:check-interlocking-joint-angle-validity = `[method]
&key = (angle-thre 0.001) (interlocking-joint-pairs (send self :interlocking-joint-pairs))

Check if all interlocking joint pairs are same values.

:update-descendants &rest args

:find-link-route to &optional from

:make-joint-min-max-table l0 l1 joint0 joint1 &key (fat 0) (fat2 nil) (debug nil) (margin 0.0) (overwrite-collision-model nil)

:make-min-max-table-using-collision-check l0 l1 joint0 joint1 joint-range0 joint-range1 min-joint0 min-joint1 fat fat2 debug margin

:plot-joint-min-max-table-common joint0 joint1

:calc-target-axis-dimension rotation-axis translation-axis

:calc-union-link-list link-list

:calc-target-joint-dimension link-list

:calc-inverse-jacobian jacobi &rest args &key ((:manipulability-limit ml) 0.1) ((:manipulability-gain mg) 0.001) weight debug-view ret wmat tmat umat umat2 mat-tmp mat-tmp-rc tmp-mrr tmp-mrr2 &allow-other-keys

:calc-gradh-from-link-list link-list &optional (res (instantiate float-vector (length link-list)))

:calc-joint-angle-speed union-vel &rest args &key angle-speed (angle-speed-blending 0.5) jacobi jacobi# null-space i-j#j debug-view weight wmat tmp-len tmp-len2 fik-len &allow-other-keys

:calc-joint-angle-speed-gain union-link-list dav periodic-time

:collision-avoidance-links &optional l

:collision-avoidance-link-pair-from-link-list link-lists &key obstacles ((:collision-avoidance-links collision-links) collision-avoidance-links) debug

:collision-avoidance-calc-distance &rest args &key union-link-list (warnp t) ((:collision-avoidance-link-pair pair-list)) ((:collision-distance-limit distance-limit) 10) &allow-other-keys

:collision-avoidance-args pair link-list

:collision-avoidance &rest args &key avoid-collision-distance avoid-collision-joint-gain avoid-collision-null-gain ((:collision-avoidance-link-pair pair-list)) (union-link-list) (link-list) (weight) (fik-len (send self :calc-target-joint-dimension union-link-list)) debug-view &allow-other-keys

:move-joints union-vel &rest args &key union-link-list (periodic-time 0.05) (joint-args) (debug-view nil) (move-joints-hook) &allow-other-keys

:find-joint-angle-limit-weight-old-from-union-link-list union-link-list

:reset-joint-angle-limit-weight-old union-link-list

:calc-weight-from-joint-limit avoid-weight-gain fik-len link-list union-link-list debug-view weight tmp-weight tmp-len

:calc-inverse-kinematics-weight-from-link-list link-list &key (avoid-weight-gain 1.0) (union-link-list (send self :calc-union-link-list link-list)) (fik-len (send self :calc-target-joint-dimension union-link-list)) (weight (fill (instantiate float-vector fik-len) 1)) (additional-weight-list) (debug-view) (tmp-weight (instantiate float-vector fik-len)) (tmp-len (instantiate float-vector fik-len))

:calc-nspace-from-joint-limit avoid-nspace-gain union-link-list weight debug-view tmp-nspace

:calc-inverse-kinematics-nspace-from-link-list link-list &key (avoid-nspace-gain 0.01) (union-link-list (send self :calc-union-link-list link-list)) (fik-len (send self :calc-target-joint-dimension union-link-list)) (null-space) (debug-view) (additional-nspace-list) (cog-gain 0.0) (target-centroid-pos) (centroid-offset-func) (cog-translation-axis :z) (cog-null-space nil) (weight (fill (instantiate float-vector fik-len) 1.0)) (update-mass-properties t) (tmp-nspace (instantiate float-vector fik-len))

:inverse-kinematics-args &rest args &key union-link-list rotation-axis translation-axis additional-jacobi-dimension &allow-other-keys

:draw-collision-debug-view **

:ik-convergence-check success dif-pos dif-rot rotation-axis translation-axis thre rthre centroid-thre target-centroid-pos centroid-offset-func cog-translation-axis &key (update-mass-properties t)

:calc-vel-from-pos dif-pos translation-axis &rest args &key (p-limit 100.0) (tmp-v0 (instantiate float-vector 0)) (tmp-v1 (instantiate float-vector 1)) (tmp-v2 (instantiate float-vector 2)) (tmp-v3 (instantiate float-vector 3)) &allow-other-keys

:calc-vel-from-rot dif-rot rotation-axis &rest args &key (r-limit 0.5) (tmp-v0 (instantiate float-vector 0)) (tmp-v1 (instantiate float-vector 1)) (tmp-v2 (instantiate float-vector 2)) (tmp-v3 (instantiate float-vector 3)) &allow-other-keys

:collision-check-pairs &key ((:links ls) (cons (car links) (all-child-links (car links))))

:self-collision-check &key (mode :all) (pairs (send self :collision-check-pairs)) (collision-func ’collision-check)

:plot-joint-min-max-table joint0 joint1

Plot joint min max table on Euslisp window.

:link-list to &optional from

Find link list from to link to from link.

:angle-vector &optional vec (angle-vector (instantiate float-vector (calc-target-joint-dimension joint-list)))

Returns angle-vector of this object, if vec is given, it updates angles of all joint. If given angle-vector violate min/max range, the value is modified.

:faces **

Return faces of this object.

:bodies &rest args

Return bodies of this object. If args is given it passed to all bodies

:end-coords name

Returns end-coords with given name

:joint name

Return a joint with given name.

:link name

Return a link with given name.

:joint-list &rest args

Returns joint list, or args is passed to joints

:links &rest args

Returns links, or args is passed to links

:init-ending **

This method is to called finalize the instantiation of the cascaded-link. This update bodies and child-link and parent link from joint-list

:init = `[method]
&rest args &key = name &allow-other-keys

Create cascaded-link.

:plot-joint-min-max-table-common joint0 joint1

:make-min-max-table-using-collision-check l0 l1 joint0 joint1 joint-range0 joint-range1 min-joint0 min-joint1 fat fat2 debug margin

:make-joint-min-max-table l0 l1 joint0 joint1 &key (fat 0) (fat2 nil) (debug nil) (margin 0.0) (overwrite-collision-model nil)

:find-link-route to &optional from

:update-descendants &rest args

:check-interlocking-joint-angle-validity = `[method]
&key = (angle-thre 0.001) (interlocking-joint-pairs (send self :interlocking-joint-pairs))

Check if all interlocking joint pairs are same values.

:interlocking-joint-pairs **

Interlocking joint pairs.
pairs are (list (cons joint0 joint1) ... )
If users want to use interlocking joints, please overwrite this method.

:set-midpoint-for-interlocking-joints &key (interlocking-joint-pairs (send self :interlocking-joint-pairs))

Set interlocking joints at mid point of each joint angle.

:calc-vel-for-interlocking-joints link-list &key (interlocking-joint-pairs (send self :interlocking-joint-pairs))

Calculate 0 velocity for keeping interlocking joint at the same joint angle.

:calc-jacobian-for-interlocking-joints link-list &key (interlocking-joint-pairs (send self :interlocking-joint-pairs))

Calculate jacobian to keep interlocking joint velocity same.
dtheta_0 = dtheta_1 =>[... 0 1 0 ... 0 -1 0 .... ][...dtheta_0...dtheta_1...]
:inverse-kinematics-for-closed-loop-forward-kinematics = `[method]
target-coords &rest args &key = (move-target) (link-list) (move-joints-hook) (additional-weight-list) (constrained-joint-list) (constrained-joint-angle-list) (min-loop 2) &allow-other-keys
Solve inverse-kinematics for closed loop forward kinematics.
Move move-target to target-coords with link-list.
link-list loop should be close when move-target reaches target-coords.
constrained-joint-list is list of joints specified given joint angles in closed loop.
constrained-joint-angle-list is list of joint-angle for constrained-joint-list.
:calc-grasp-matrix = `[method]
contact-points &key = (ret (make-matrix 6 (6 (length contact-points)))) (contact-rots (mapcar #’(lambda (r) (unit-matrix 3)) contact-points))
Calc grasp matrix.
Grasp matrix is defined as
| E_3 0 E_3 0 ... |
| p1x E_3 p2x E_3 ... |
Arguments:
contact-points is list of contact points[mm].
contact-rots is list of contact coords rotation[rad].
If contact-rots is specified, grasp matrix as follow:
| R1 0 R2 0 ... |
| p1xR1 R1 p2xR2 R2 ... |
:inverse-kinematics = `[method]
target-coords &rest args &key = (stop 50) (link-list) (move-target) (debug-view) (warnp t) (revert-if-fail t) (rotation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t)))) (translation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t)))) (joint-args) (thre (cond ((atom move-target) 1) (t (make-list (length move-target) :initial-element 1)))) (rthre (cond ((atom move-target) (deg2rad 1)) (t (make-list (length move-target) :initial-element (deg2rad 1))))) (union-link-list) (centroid-thre 1.0) (target-centroid-pos) (centroid-offset-func) (cog-translation-axis :z) (cog-null-space nil) (dump-command :fail-only) (periodic-time 0.5) (check-collision) (additional-jacobi) (additional-vel) &allow-other-keys
Move move-target to target-coords.
;; target-coords, link-list and move-target need to be given.
;; target-coords, move-target, rotation-axis, translation-axis, link-list
;; ->both list and atom OK.
:target-coords
  The coordinate of the target, or a function that returns coordinates. When a function is given, it is called in every IK loop as (funcall target-coords). Use a list of targets to solve the IK relative to multiple end links simultaneously.
:stop
  Maximum number for IK iteration. Default is 50.
:link-list
  List of links to control. When the target-coords is list, this should be a list of lists.
:move-target
  Specify end-effector coordinate. When the target-coords is list, this should be list too.
:debug-view
  Set t to show debug message and visualization. Use :no-message to just show the irtview image. Default is nil.
:warnp
  Set nil to not display debug message when the IK failed. Default is t.
:revert-if-fail
  Set nil to keep the angle posture of IK solve iteration. Default is t, which return to original position when IK fails.
:rotation-axis
  Use nil for position only IK. :x, :y, :z for the constraint around axis with plus direction, :-x :-y :-z for axis with minus direction. :zz :yy :zz for direction free axis. :xm :ym :zm for allowing rotation with respect to mirror direction. When the target-coords is list, this should be list too. Default is t.
:translation-axis
  :x :y :z for constraint along the x, y, z axis. :xy :yz :zx for plane. Default is t.
:joint-args
  Arguments passed to joint as (sendjoint :joint-angle angle :relative t joint-args). Default nil.
:thre
  Threshold for position error to terminate IK iteration. Default is 1 [mm].
:rthre
  Threshold for rotation error to terminate IK iteration. Default is 0.017453 [rad] (1 deg).
:union-link-list
  a function that returns union of link-list called as (funcall union-link-list link-list). Default is (send self :calc-union-link-list link-list).
:centroid-thre
  Threshold for centroid position error to terminate IK iteration. Default is 1 [mm].
:target-centroid-pos
  The float-vector of the target centroid position. Default is nil.
:centroid-offset-func
  A function that returns centroid position. This function is called in each IK loop as (funcall centroid-offset-func). Default is (send self :centroid).
:cog-translation-axis
  :x :y :z for constraint along the x, y, z axis. :xy :yz :zx for plane. t for point. Default is :z.
:cog-null-space
  t: centroid position task is solved in null space of the main task. Default is nil.
:dump-command
 should be t, nil, :always, :fail-only, :always-with-debug-log, or :fail-only-with-debug-log. Log are success/fail log and ik debug information log.
   t or :always : dump log both in success and fail (for success/fail log).
   :always-with-debug-log : dump log both in success and fail (for success/fail log and ik debug information log).
   :fail-only : dump log only in fail (for success/fail log).
   :always-with-debug-log : dump log only in fail (for success/fail log and ik debug information log).
   nil : do not dump log.
:periodic-time
  The amount of joint angle modification in each IK loop is scaled not to violate joint velocity limit times :periodic-time. Default is 0.5[s].
:check-collision
  Set t to return false when self collision occurs at found IK solution. Default is nil. To avoid collision within IK loop, use set links to collision-avoidance-links slot of cascaded-link.
:additional-jacobi
  The jacobian of the additional main task, or a function that returns the jacobian. When a function is given, it is called in every IK loop as (funcall additional-jacobi link-list). Use a list of additional-jacobi to solve the IK for multiple additional task. Default is nil.
:additional-vel
  The velocity of additional main task, or a function that returns the velocity. When a function is given, it is called in every IK loop as (funcall additional-vel link-list). The velocity should be expressed in the same coordinates as corresponding additional-jacobi. When the additional-jacobi is list, this should be a list of same length. Default is nil.
other-keys
  function :inverse-kinematics-loop is internally called and args are passed to it. See the explanation of :inverse-kinematics-loop.
:inverse-kinematics-loop = `[method]
dif-pos dif-rot &rest args &key = (stop 1) (loop 0) link-list move-target (rotation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t)))) (translation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t)))) (thre (cond ((atom move-target) 1) (t (make-list (length move-target) :initial-element 1)))) (rthre (cond ((atom move-target) (deg2rad 1)) (t (make-list (length move-target) :initial-element (deg2rad 1))))) (dif-pos-ratio 1.0) (dif-rot-ratio 1.0) union-link-list target-coords (jacobi) (additional-check) (additional-jacobi) (additional-vel) (centroid-thre 1.0) (target-centroid-pos) (centroid-offset-func) (cog-translation-axis :z) (cog-null-space nil) (cog-gain 1.0) (min-loop (/ stop 10)) debug-view ik-args &allow-other-keys
:inverse-kinematics-loop is one loop calculation for :inverse-kinematics.
In this method, joint position difference satisfying workspace difference (dif-pos, dif-rot) are calculated and euslisp model joint angles are updated.
Optional arguments:
  :dif-pos-ratio
   Ratio of spacial velocity used in calculation of joint position difference to workspace difference (after :p-limit applied). Default is 1.0.
  :dif-rot-ratio
   Ratio of angular velocity used in calculation of joint position difference to workspace difference (after :r-limit applied). Default is 1.0.
  :jacobi
   A jacobian of all move-target or a function that returns the jacobian. When a function is given, It is called in every IK loop as (funcall jacobi link-list move-target translation-axis rotation-axis). Default is (sendself :calc-jacobian-from-link-list link-list :translation-axis translation-axis :rotation-axis rotation-axis :move-target move-target method-args).
  :additional-check
   This argument is to add optional best-effort convergence conditions. Default is nil (no additional check). :additional-check should be function or lambda.
   best-effort =>
    In :inverse-kinematics-loop, ’success’ is overwritten by ’(and success additional-check)’
    In :inverse-kinematics, ’success is not overwritten.
    So, :inverse-kinematics-loop wait until ’:additional-check’ becomes ’t’ as possible,
    but ’:additional-check’ is neglected in the final :inverse-kinematics return.
  :cog-gain
   Ratio of centroid velocity used in calculation of joint position difference to centroid position difference. max 1.0. Default is 1.0.
  :min-loop
   Minimam loop count. Defalt (/ stop 10).
   If integer is specified, :inverse-kinematics-loop does returns :ik-continues and continuing solving IK.
   If min-loop is nil, do not consider loop counting for IK convergence.
  other-keys
   :move-joints-avoidance is internally called and args are passed to it. See the explanation of :move-joints-avoidance.
   :p-limit
    Maximum spacial velocity of each move-target in one IK loop. Default is 100.0[mm].
   :r-limit
    Maximum angular velocity of each move-target in one IK loop. Default is 0.5[rad].
:move-joints-avoidance = `[method]
union-vel &rest args &key = union-link-list link-list (fik-len (send self :calc-target-joint-dimension union-link-list)) (weight (fill (instantiate float-vector fik-len) 1)) (null-space) (avoid-nspace-gain 0.01) (avoid-weight-gain 1.0) (avoid-collision-distance 200) (avoid-collision-null-gain 1.0) (avoid-collision-joint-gain 1.0) ((:collision-avoidance-link-pair pair-list) (send self :collision-avoidance-link-pair-from-link-list link-list :obstacles (cadr (memq :obstacles args)) :debug (cadr (memq :debug-view args)))) (cog-gain 0.0) (target-centroid-pos) (centroid-offset-func) (cog-translation-axis :z) (cog-null-space nil) (additional-weight-list) (additional-nspace-list) (tmp-len (instantiate float-vector fik-len)) (tmp-len2 (instantiate float-vector fik-len)) (tmp-weight (instantiate float-vector fik-len)) (tmp-nspace (instantiate float-vector fik-len)) (tmp-mcc (make-matrix fik-len fik-len)) (tmp-mcc2 (make-matrix fik-len fik-len)) (debug-view) (jacobi) &allow-other-keys
:move-joints-avoidance is called in :inverse-kinematics-loop. In this method, calculation of joint position difference are executed and joint positon are moved.
Optional arguments:
  :weight
   float-vector of inverse weight of velocity of each joint or a function which returns the float-vector or a list which returns the float-vector. Length of the float-vector should be same as the number of columns of the jacobian. If :weight is a function or a list, it is called in each IK loop as (funcall weight union-link-list) or (eval weight). :weight is used in calculation of weighted norm of joint velocity for sr-inverse. Default is the float-vector filled with 1.
  :null-space
   float-vector of joint velocity or a function which returns the float-vector or a list which returns the float-vector. Length of the float-vector should be same as the number of columns of the jacobian. If :null-space is a function or a list, it is called in each IK loop as (funcall null-space) or (eval null-space). This joint velocity is applied in null space of main task in each IK loop. Default is nil.
  :avoid-nspace-gain
  gain of joint velocity to avoid joint limit applied in null space of main task in each IK loop. The avoiding velocity is calculated as \((((t\_max + t\_min)/2 - t) / ((t\_max - t\_min)/2))^2\). Default is 0.01.
  :avoid-weight-gain
   gain of dH/dt in calcuration of avoiding joint limits weight. :weight is devided by this avoiding joint limits weight. Default is 1.0.
   If :avoid-nspace-gain is 0, :weight is multipled by :weight instead.
  :avoid-collision-distance
   yellow zone. 0.1avoid-collision-distance is regarded as orange zone.
   If :avoid-collision-joint-gain is smaller than or equal to 0.0, yellow zone and orange zone become inactive. Default is 200[mm].
  :avoid-collision-null-gain
   \(k\_{null}\). Default is 1.0.
  :avoid-collision-joint-gain
   \(k\_{joint}\). Default is 1.0.
  :collision-avoidance-link-pair
   (list (list link1 link2) (list link3 link4) ...) with any length. Collision between paired links is cared. Default is (send self :collision-avoidance-link-pair-from-link-list link-list :obstacles (cadr (memq :obstacles args))).
  :additional-weight-list
   (list (list target-link1 additional-weight1) (list target-link2 additional-weight2) ...) with any length. The component of :weight corresponding to the parent joint of target-link is scaled by additional-weight. additional-weight should be float (if 1 dof), float-vector with length of the joint dof, or a function which returns the float or float-vector. if additional-weight is a function, it is called in each IK loop as (funcall additional-weight). Default is nil.
  :additional-nspace-list
   (list (list target-link1 var1) (list target-link2 var2) ...) with any length. In each IK loop, the parent joint of target-link is moved by the amount of var in null space of main task. var should be float (if 1dof), float-vector with the same length of the target joint dof, or a function which returns the float or float-vector.If var is float-vector, it is called in each IK loop as (funcall var). Default is nil.
  other-keys
   :manipulability-limit
    If manipulability of jacobian is smaller than manipulability-limit, diagonal matrix is added in calculation of sr-inverse. Default is 0.1.
  :manipulability-gain
   Weight of diagonal matrix in calculation of sr-inverse. Weight is calculated as (manipulability-gain (expt (- 1.0 (/ manipulability manipulability-limit)) 2)). Default is 0.001.
   :collision-distance-limit
    Threshold for collision detection. If collision is detected, the distance between the colliding links is considered to be :collision-distance-limit instead of actual distance. Default is 10[mm].
   :move-joints-hook
    A function which is called right after joints are moved in each IK loop as (funcall move-joints-hook). Default is nil.
:calc-jacobian-from-link-list = `[method]
link-list &rest args &key = move-target (transform-coords move-target) (rotation-axis (cond ((atom move-target) nil) (t (make-list (length move-target))))) (translation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t)))) (col-offset 0) (dim (send self :calc-target-axis-dimension rotation-axis translation-axis)) (fik-len (send self :calc-target-joint-dimension link-list)) fik (tmp-v0 (instantiate float-vector 0)) (tmp-v1 (instantiate float-vector 1)) (tmp-v2 (instantiate float-vector 2)) (tmp-v3 (instantiate float-vector 3)) (tmp-v3a (instantiate float-vector 3)) (tmp-v3b (instantiate float-vector 3)) (tmp-m33 (make-matrix 3 3)) &allow-other-keys
Calculate jacobian matrix from link-list and move-target. Jacobian is represented in :transform-coords. Unit system is [m] or [rad], not [mm] or [deg].
Joint order for this jacobian matrix follows link-list order. Joint torque[Nm] order is also the same.
Ex1. One-Arm
(setq rarm-link-list(send robot:link-list (send robot:rarm :end-coords :parent)))
(send-all rarm-link-list:joint)
Ex2. Two-Arm
(setq arms-link-list(mapcar #’(lambda (l) (send robot:link-list (send robotl :end-coords :parent))) ’(:rarm :larm)))
(send-all (send robot:calc-union-link-list arms-link-list) :joint)

:self-collision-check &key (mode :all) (pairs (send self :collision-check-pairs)) (collision-func ’collision-check)

:collision-check-pairs &key ((:links ls) (cons (car links) (all-child-links (car links))))

:calc-vel-from-rot dif-rot rotation-axis &rest args &key (r-limit 0.5) (tmp-v0 (instantiate float-vector 0)) (tmp-v1 (instantiate float-vector 1)) (tmp-v2 (instantiate float-vector 2)) (tmp-v3 (instantiate float-vector 3)) &allow-other-keys

:calc-vel-from-pos dif-pos translation-axis &rest args &key (p-limit 100.0) (tmp-v0 (instantiate float-vector 0)) (tmp-v1 (instantiate float-vector 1)) (tmp-v2 (instantiate float-vector 2)) (tmp-v3 (instantiate float-vector 3)) &allow-other-keys

:ik-convergence-check success dif-pos dif-rot rotation-axis translation-axis thre rthre centroid-thre target-centroid-pos centroid-offset-func cog-translation-axis &key (update-mass-properties t)

:draw-collision-debug-view **

:inverse-kinematics-args &rest args &key union-link-list rotation-axis translation-axis additional-jacobi-dimension &allow-other-keys

:calc-inverse-kinematics-nspace-from-link-list link-list &key (avoid-nspace-gain 0.01) (union-link-list (send self :calc-union-link-list link-list)) (fik-len (send self :calc-target-joint-dimension union-link-list)) (null-space) (debug-view) (additional-nspace-list) (cog-gain 0.0) (target-centroid-pos) (centroid-offset-func) (cog-translation-axis :z) (cog-null-space nil) (weight (fill (instantiate float-vector fik-len) 1.0)) (update-mass-properties t) (tmp-nspace (instantiate float-vector fik-len))

:calc-nspace-from-joint-limit avoid-nspace-gain union-link-list weight debug-view tmp-nspace

:calc-inverse-kinematics-weight-from-link-list link-list &key (avoid-weight-gain 1.0) (union-link-list (send self :calc-union-link-list link-list)) (fik-len (send self :calc-target-joint-dimension union-link-list)) (weight (fill (instantiate float-vector fik-len) 1)) (additional-weight-list) (debug-view) (tmp-weight (instantiate float-vector fik-len)) (tmp-len (instantiate float-vector fik-len))

:calc-weight-from-joint-limit avoid-weight-gain fik-len link-list union-link-list debug-view weight tmp-weight tmp-len

:reset-joint-angle-limit-weight-old union-link-list

:find-joint-angle-limit-weight-old-from-union-link-list union-link-list

:move-joints union-vel &rest args &key union-link-list (periodic-time 0.05) (joint-args) (debug-view nil) (move-joints-hook) &allow-other-keys

:collision-avoidance &rest args &key avoid-collision-distance avoid-collision-joint-gain avoid-collision-null-gain ((:collision-avoidance-link-pair pair-list)) (union-link-list) (link-list) (weight) (fik-len (send self :calc-target-joint-dimension union-link-list)) debug-view &allow-other-keys

:collision-avoidance-args pair link-list

:collision-avoidance-calc-distance &rest args &key union-link-list (warnp t) ((:collision-avoidance-link-pair pair-list)) ((:collision-distance-limit distance-limit) 10) &allow-other-keys

:collision-avoidance-link-pair-from-link-list link-lists &key obstacles ((:collision-avoidance-links collision-links) collision-avoidance-links) debug

:collision-avoidance-links &optional l

:calc-joint-angle-speed-gain union-link-list dav periodic-time

:calc-joint-angle-speed union-vel &rest args &key angle-speed (angle-speed-blending 0.5) jacobi jacobi# null-space i-j#j debug-view weight wmat tmp-len tmp-len2 fik-len &allow-other-keys

:calc-gradh-from-link-list link-list &optional (res (instantiate float-vector (length link-list)))

:calc-inverse-jacobian jacobi &rest args &key ((:manipulability-limit ml) 0.1) ((:manipulability-gain mg) 0.001) weight debug-view ret wmat tmat umat umat2 mat-tmp mat-tmp-rc tmp-mrr tmp-mrr2 &allow-other-keys

:calc-target-joint-dimension link-list

:calc-union-link-list link-list

:calc-target-axis-dimension rotation-axis translation-axis

eusmodel-validity-check robot

Check if the robot model is validate

calc-jacobian-default-rotate-vector paxis world-default-coords child-reverse transform-coords tmp-v3 tmp-m33

calc-jacobian-rotational fik row column joint paxis child-link world-default-coords child-reverse move-target transform-coords rotation-axis translation-axis tmp-v0 tmp-v1 tmp-v2 tmp-v3 tmp-v3a tmp-v3b tmp-m33

calc-jacobian-linear fik row column joint paxis child-link world-default-coords child-reverse move-target transform-coords rotation-axis translation-axis tmp-v0 tmp-v1 tmp-v2 tmp-v3 tmp-v3a tmp-v3b tmp-m33

calc-angle-speed-gain-scalar j dav i periodic-time

calc-angle-speed-gain-vector j dav i periodic-time

all-child-links s &optional (pred #’identity)

calc-dif-with-axis dif axis &optional tmp-v0 tmp-v1 tmp-v2

calc-target-joint-dimension joint-list

calc-joint-angle-min-max-for-limit-calculation j kk jamm

joint-angle-limit-weight j-l &optional (res (instantiate float-vector (calc-target-joint-dimension j-l)))

joint-angle-limit-nspace j-l &optional (res (instantiate float-vector (calc-target-joint-dimension j-l)))

calc-jacobian-from-link-list-including-robot-and-obj-virtual-joint link-list move-target obj-move-target robot &key (rotation-axis ’(t t)) (translation-axis ’(t t)) (fik (make-matrix (send robot :calc-target-axis-dimension rotation-axis translation-axis) (send robot :calc-target-joint-dimension link-list)))

append-obj-virtual-joint link-list target-coords &key (joint-class 6dof-joint) (joint-args) (vplink) (vplink-coords) (vclink-coords)

append-multiple-obj-virtual-joint link-list target-coords &key (joint-class ’(6dof-joint)) (joint-args ’(nil)) (vplink) (vplink-coords) (vclink-coords)

eusmodel-validity-check-one robot

line

:super = ** propertied-object**
:slots pvert nvert

:worldcoords **

Return a coordinates on the midpoint of the end points

coordinates

:super = ** propertied-object**
:slots rot pos

:difference-rotation coords &key (geometry::rotation-axis t)

return difference in rotation of given coords, rotation-axis can take (:x, :y, :z, :xx, :yy, :zz, :xm, :ym, :zm)

:difference-position coords &key (geometry::translation-axis t)

return difference in position of given coords, translation-axis can take (:x, :y, :z, :xy, :yz, :zx).

:axis geometry::axis

coordinates

:super = ** propertied-object**
:slots rot pos

:move-coords geometry::target geometry::at

fix ’at’ coords on ’self’ to ’target’

:transform geometry::c &optional (geometry::wrt :local)

:transformation geometry::c2 &optional (geometry::wrt :local)

:move-to geometry::c &optional (geometry::wrt :local) &aux geometry::cc

cascaded-coords

:super = ** coordinates**
:slots rot pos parent descendants worldcoords manager changed

coordinates

:super = ** propertied-object**
:slots rot pos

cascaded-coords

:super = ** coordinates**
:slots rot pos parent descendants worldcoords manager changed

coordinates

:super = ** propertied-object**
:slots rot pos

cascaded-coords

:super = ** coordinates**
:slots rot pos parent descendants worldcoords manager changed

bodyset

:super = ** cascaded-coords**
:slots (geometry::bodies :type cons)
:init = `[method]
coords &rest args &key = (name (intern (format nil bodyset A (system:address self)) KEYWORD)) ((:bodies geometry::bs)) &allow-other-keys

Create bodyset object

:bodies &rest args

:faces **

:worldcoords **

:draw-on &rest args

:init = `[method]
coords &rest args &key = (name (intern (format nil bodyset A (system:address self)) KEYWORD)) ((:bodies geometry::bs)) &allow-other-keys

Create bodyset object

:draw-on &rest args

:worldcoords **

:faces **

:bodies &rest args

midcoords geometry::p geometry::c1 geometry::c2

Returns mid (or p) coordinates of given two cooridnates c1 and c2

orient-coords-to-axis geometry::target-coords geometry::v &optional (geometry::axis :z) (geometry::eps epsilon)

orient ’axis’ in ’target-coords’ to the direction specified by ’v’ destructively.
’v’ must be non-zero vector.

geometry::face-to-triangle-aux geometry::f

triangulate the face.

geometry::face-to-triangle geometry::f

convert face to set of triangles.

geometry::face-to-tessel-triangle geometry::f geometry::num &optional (epsilon1.000000e-10)

return polygon if triangable, return nil if it is not.

body-to-faces geometry::abody

return triangled faces of given body

make-sphere geometry::r &rest args

make sphere of given r

make-ring geometry::ring-radius geometry::pipe-radius &rest args &key (geometry::segments 16)

make ring of given ring and pipe radius

make-fan-cylinder = `[function]
geometry::radius geometry::height &rest args &key = (geometry::segments 12) (angle 2pi) (geometry::mid-angle (/ angle 2.0))
make a cylinder whose base face is a fan. the angle of fan
is defined by :angle keyword. and, the csg of the returned body is
(:cylinder radius height segments angle)

x-of-cube geometry::cub

return x of cube.

y-of-cube geometry::cub

return y of cube.

z-of-cube geometry::cub

return z of cube.

height-of-cylinder geometry::cyl

return height of cylinder.

radius-of-cylinder geometry::cyl

return radius of cylinder.

radius-of-sphere geometry::sp

return radius of shape.

geometry::make-faceset-from-vertices geometry::vs

create faceset from vertices.

matrix-to-euler-angle geometry::m geometry::axis-order

return euler angle from matrix.

geometry::quaternion-from-two-vectors geometry::a geometry::b

Comupute quaternion which rotate vector a into b.

transform-coords geometry::c1 geometry::c2 &optional (geometry::c3 (let ((geometry::dim (send geometry::c1 :dimension))) (instance coordinates :newcoords (unit-matrix geometry::dim) (instantiate float-vector geometry::dim))))

geometry::face-to-triangle-rest-polygon geometry::f geometry::num geometry::edgs

geometry::face-to-triangle-make-simple geometry::f

body-to-triangles geometry::abody &optional (geometry::limit 50)

geometry::triangle-to-triangle geometry::aface &optional (geometry::limit 50)

robot-model

:super = ** cascaded-link**
:slots larm-end-coords rarm-end-coords lleg-end-coords rleg-end-coords head-end-coords torso-end-coords larm-root-link rarm-root-link lleg-root-link rleg-root-link head-root-link torso-root-link larm-collision-avoidance-links rarm-collision-avoidance-links larm rarm lleg rleg torso head force-sensors imu-sensors cameras support-polygons

:camera sensor-name

Returns camera with given name

:force-sensor sensor-name

Returns force sensor with given name

:imu-sensor sensor-name

Returns imu sensor of given name

:force-sensors **

Returns force sensors.

:imu-sensors **

Returns imu sensors.

:cameras **

Returns camera sensors.

:look-at-hand l/r

look at hand position, l/r supports :rarm, :larm, :arms, and ’(:rarm :larm)

:inverse-kinematics = `[method]
target-coords &rest args &key = look-at-target (move-target) (link-list (if (atom move-target) (send self :link-list (send move-target :parent)) (mapcar #’(lambda (mt) (send self :link-list (send mt :parent))) move-target))) &allow-other-keys
solve inverse kinematics, move move-target to target-coords
target-coords and move-target should be given.
link-list is set by default based on move-target ->root link link-list
:look-at-target
  target head looks at. This task is best-effort and only head joints are used. :look-at-target supports t, nil, float-vector, coords, list of float-vector, list of coords.
other-keys
  :inverse-kinematics internally calls :inverse-kinematics of cascaded-cords class and args are passed to it. See the explanation of :inverse-kinematics of cascaded-cords class.
:inverse-kinematics-loop = `[method]
dif-pos dif-rot &rest args &key = target-coords debug-view look-at-target (move-target) (link-list (if (atom move-target) (send self :link-list (send move-target :parent)) (mapcar #’(lambda (mt) (send self :link-list (send mt :parent))) move-target))) &allow-other-keys
move move-target using dif-pos and dif-rot,
look-at-target suppots t, nil, float-vector, coords, list of float-vector, list of coords
link-list is set by default based on move-target ->root link link-list
:inverse-kinematics-loop internally calls :inverse-kinematics-loop function of cascaded-coords class. See the explanation of :inverse-kinematics-loop in cascaded-coords class.

:look-at-target look-at-target &key (target-coords)

move robot head to look at targets, look-at-target support t/nil float-vector coordinates, center of list of float-vector or list of coordinates

:init-pose **

Set robot to initial posture.

:torque-vector = `[method]
&key = (force-list) (moment-list) (target-coords) (debug-view nil) (calc-statics-p t) (dt 0.005) (av (send self :angle-vector)) (root-coords (send (car (send self :links)) :copy-worldcoords)) (calc-torque-buffer-args (send self :calc-torque-buffer-args)) (distribute-total-wrench-to-torque-method (if (and (not (every #’null (send self :legs))) (not (and force-list moment-list target-coords))) :distribute-total-wrench-to-torque-method-default))

Returns torque vector

:calc-force-from-joint-torque = `[method]
limb all-torque &key = (move-target (send self limb :end-coords)) (use-torso)

Calculates end-effector force and moment from joint torques.

:fullbody-inverse-kinematics = `[method]
target-coords &rest args &key = (move-target) (link-list) (min (float-vector -500 -500 -500 -20 -20 -10)) (max (float-vector 500 500 25 20 20 10)) (root-link-virtual-joint-weight #f(0.1 0.1 0.1 0.1 0.5 0.5)) (target-centroid-pos (apply #’midpoint 0.5 (send self :legs :end-coords :worldpos))) (cog-gain 1.0) (cog-translation-axis :z) (centroid-offset-func nil) (centroid-thre 5.0) (additional-weight-list) (joint-args nil) (cog-null-space nil) (min-loop 2) &allow-other-keys
fullbody inverse kinematics for legged robot.
necessary args : target-coords, move-target, and link-list must include legs’ (or leg’s) parameters
ex. (send robot:fullbody-inverse-kinematics (list rarm-tc rleg-tc lleg-tc) :move-target (list rarm-mt rleg-mt lleg-mt) :link-list (list rarm-ll rleg-ll lleg-ll))
:min
  lower position limit of root link virtual joint (x y z roll pitch yaw). Default is #f(-500[mm] -500[mm] -500[mm] -20[deg] -20[deg] -10[deg]).
:max
  upper position limit of root link virtual joint (x y z roll pitch yaw). Default is #f(500[mm] 500[mm] 25[mm] 20[deg] 20[deg] 10[deg]).
:root-link-virtual-joint-weight
  float-vector of inverse weight of velocity of root link virtual joint or a function which returns the float-vector (x y z roll pitch yaw). This works in the same way as :additional-weight-list in cascaded-coords::inverse-kinematics. Default is #f(0.1 0.1 0.1 0.1 0.5 0.5).
:joint-args
  list of other arguments passed to :init function of root link virtual joint (6dof-joint class).
   :max-joint-velocity
    limit of velocity of root link virtual joint (x y z roll pitch yaw). Default is #f((/ 0.08 0.05)[m/s] (/ 0.08 0.05)[m/s] (/ 0.08 0.05)[m/s] (/ pi 4)[rad/s] (/ pi 4)[rad/s] (/ pi 4)[rad/s]))
other-keys
  :fullbody-inverse-kinematics internally calls :inverse-kinematics and args are passed to it. See the explanation of :inverse-kinematics.

:print-vector-for-robot-limb vec

Print angle vector with limb alingment and limb indent.
For example, if robot is rarm, larm, and torso, print result is:
#f(
rarm-j0 ... rarm-jN
larm-j0 ... larm-jN
torso-j0 ... torso-jN
)
:calc-zmp-from-forces-moments = `[method]
forces moments &key = (wrt :world) (limbs (if (send self :force-sensors) (remove nil (mapcar #’(lambda (fs) (find-if #’(lambda (l) (equal fs (car (send self l :force-sensors)))) ’(:rleg :lleg))) (send self :force-sensors))) ’(:rleg :lleg))) (force-sensors (mapcar #’(lambda (l) (car (send self l :force-sensors))) limbs)) (cop-coords (mapcar #’(lambda (l) (send self l :end-coords)) limbs)) (fz-thre 0.001) (limb-cop-fz-list (mapcar #’(lambda (fs f m cc) (let ((fsp (scale 0.001 (send fs :worldpos))) (nf (send fs :rotate-vector f)) (nm (send fs :rotate-vector m))) (send self :calc-cop-from-force-moment nf nm fs cc :fz-thre fz-thre :return-all-values t))) force-sensors forces moments cop-coords))
Calculate zmp[mm] from sensor local forces and moments
If force_z is large, zmp can be defined and returns 3D zmp.
Otherwise, zmp cannot be defined and returns nil.

:foot-midcoords &optional (mid 0.5)

Calculate midcoords of :rleg and :lleg end-coords.
In the following codes, leged robot is assumed.
:fix-leg-to-coords = `[method]
fix-coords &optional (l/r :both) &key = (mid 0.5) &allow-other-keys
Fix robot’s legs to a coords
In the following codes, leged robot is assumed.
:move-centroid-on-foot = `[method]
leg fix-limbs &rest args &key = (thre (mapcar #’(lambda (x) (if (memq x ’(:rleg :lleg)) 1 5)) fix-limbs)) (rthre (mapcar #’(lambda (x) (deg2rad (if (memq x ’(:rleg :lleg)) 1 5))) fix-limbs)) (mid 0.5) (target-centroid-pos (if (eq leg :both) (apply #’midpoint mid (mapcar #’(lambda (tmp-leg) (send self tmp-leg :end-coords :worldpos)) (remove-if-not #’(lambda (x) (memq x ’(:rleg :lleg))) fix-limbs))) (send self leg :end-coords :worldpos))) (fix-limbs-target-coords (mapcar #’(lambda (x) (send self x :end-coords :copy-worldcoords)) fix-limbs)) (root-link-virtual-joint-weight #f(0.1 0.1 0.0 0.0 0.0 0.5)) &allow-other-keys
Move robot COG to change centroid-on-foot location,
leg : legs for target of robot’s centroid, which should be :both, :rleg, and :lleg.
fix-limbs : limb names which are fixed in this IK.
:calc-walk-pattern-from-footstep-list = `[method]
footstep-list &key = (default-step-height 50) (dt 0.1) (default-step-time 1.0) (solve-angle-vector-args) (debug-view nil) ((:all-limbs al) (if (send self :force-sensors) (remove nil (mapcar #’(lambda (fs) (find-if #’(lambda (l) (equal fs (car (send self l :force-sensors)))) ’(:rleg :lleg))) (send self :force-sensors))) ’(:rleg :lleg))) ((:default-zmp-offsets dzo) (mapcan #’(lambda (x) (list x (float-vector 0 0 0))) al)) (init-pose-function #’(lambda nil (send self :move-centroid-on-foot :both ’(:rleg :lleg)))) (start-with-double-support t) (end-with-double-support t) (ik-thre 1) (ik-rthre (deg2rad 1)) (q 1.0) (r 1.000000e-06) (calc-zmp t)
Calculate walking pattern from foot step list and return pattern list as a list of angle-vector, root-coords, time, and so on.
footstep-list should be given.
:footstep-list
  (list footstep1 footstep2 ...). :footstep-list can be any length. Each footstep indicates the destinations of swing legs in each step.
  footstep should be list of coordinate whose :name is identical with one swing leg and whose coords is the destination of that leg. If number of swing legs in a step is one, the footstep can be a coordinate.
  footstep1 is only for intialization and not executed.
:default-step-height
  Height of swing leg cycloid trajectories. Default is 50[mm].
:dt
  Sampling time of preview control and output walk pattern. Default is 0.1[s].
:default-step-time
  Reference time of each step. The first 10 percent and the last 10 percent of default-step-time is double support phase. Default is 1.0[s].
:solve-angle-vector-args
  :move-centroid-on-foot is used to solve IK in :calc-walk-pattern-from-footstep-list. :solve-angle-vector-args is passed to :move-centroid-on-foot in the form of (sendself :move-centroid-on-foot ... solve-angle-vector-args). Default is nil.
:debug-view
  Set t to show visualization. Default is nil.
:all-limbs
  list of limb names. In each walking step, limbs in :all-limbs but not assigned as swing legs by :footstep-list are considered to be support legs. Default is ’(:rleg :lleg) sorted in force-sensors order.
:default-zmp-offsets
  (list limbname1 offset1 limbname2 offset2 ...). :default-zmp-offsets should include every limb in :all-limbs. offset is a float-vector[mm] and local offset of reference zmp position from end-coords. Default offset is #F(0 0 0)[mm].
:init-pose-function
  A function which initialize robot’s pose. Walking pattern is generated from this initial pose. :init-pose-function is called once at the start of walking pattern generation in the form of (funcall init-pose-function). Default is #’(lambda () (send self :move-centroid-on-foot :both ’(:rleg :lleg))).
:start-with-double-support
  At the start of walking pattern generation, the initial position of reference zmp is
   t: midpoint of all-limbs.
   nil: midpoint of swing legs of footstep1.
  Default is t.
:end-with-double-support
  At the end of walking pattern generation, the final position of reference zmp is
   t: midpoint of all-limbs.
   nil: midpoint of support legs of the last footstep.
  Default is t.
:ik-thre
  Threshold for position error to terminate IK iteration. Default is 1[mm].
:ik-rthre
  Threshold for rotation error to terminate IK iteration. Default is (deg2rad 1)[rad].
:q
  Weight Q of the cost function of preview control. Default is 1.0.
:r
  Weight R of the cost function of preview control. Default is 1e-6.
:calc-zmp
  Set t to calculate resultant ZMP after IK. The calculated ZMP is visualized if :debug-view is t, and stored as czmp in return value. Default is t.

:gen-footstep-parameter &key (ratio 1.0)

Generate footstep parameter

:go-pos-params->footstep-list = `[method]
xx yy th &key = ((:footstep-parameter prm) (send self :footstep-parameter)) ((:default-half-offset defp) (cadr (memq :default-half-offset prm))) ((:forward-offset-length xx-max) (cadr (memq :forward-offset-length prm))) ((:outside-offset-length yy-max) (cadr (memq :outside-offset-length prm))) ((:rotate-rad th-max) (abs (rad2deg (cadr (memq :rotate-rad prm))))) (gen-go-pos-step-node-func #’(lambda (mc leg leg-translate-pos) (let ((cc (send (send mc :copy-worldcoords) :translate (cadr (assoc leg leg-translate-pos))))) (send cc :name leg) cc)))

Calculate foot step list from goal x position [mm], goal y position [mm], and goal yaw orientation [deg].

:go-pos-quadruped-params->footstep-list xx yy th &key (type :crawl)

Calculate foot step list for quadruped walking from goal x position [mm], goal y position [mm], and goal yaw orientation [deg].

:support-polygons **

Return support polygons.

:support-polygon name

Return support polygon.
If name is list, return convex hull of all polygons.
Otherwise, return polygon with given name

:make-default-linear-link-joint-between-attach-coords attach-coords-0 attach-coords-1 end-coords-name linear-joint-name

Make default linear arctuator module such as muscle and cylinder and append lins and joint-list.
Module includes parent-link =>(j0) =>l0 =>(j1) =>l1 (linear actuator) =>(j2) =>l2 =>end-coords.
attach-coords-0 is root side coords which linear actulator is attached to.
attach-coords-1 is end side coords which linear actulator is attached to.
end-coords-name is the name of end-coords.
linear-joint-name is the name of linear actuator.
:calc-static-balance-point = `[method]
&key = (target-points (mapcar #’(lambda (tmp-arm) (send (send self tmp-arm :end-coords) :worldpos)) ’(:rarm :larm))) (force-list (make-list (length target-points) :initial-element (float-vector 0 0 0))) (moment-list (make-list (length target-points) :initial-element (float-vector 0 0 0))) (static-balance-point-height (elt (apply #’midpoint 0.5 (send self :legs :end-coords :worldpos)) 2)) (update-mass-properties t)
Calculate static balance point which is equivalent to static extended ZMP.
The output is expressed by the world coordinates.
target-points are end-effector points on which force-list and moment-list apply.
force-list [N] and moment-list [Nm] are list of force and moment that robot receives at target-points.
static-balance-point-height is height of static balance point [mm].

:init-ending **

:rarm-end-coords **

:larm-end-coords **

:rleg-end-coords **

:lleg-end-coords **

:head-end-coords **

:torso-end-coords **

:rarm-root-link **

:larm-root-link **

:rleg-root-link **

:lleg-root-link **

:head-root-link **

:torso-root-link **

:limb limb method &rest args

:inverse-kinematics-loop-for-look-at limb &rest args

:gripper limb &rest args

:get-sensor-method sensor-type sensor-name

:get-sensors-method-by-limb sensors-type limb

:larm &rest args

:rarm &rest args

:lleg &rest args

:rleg &rest args

:head &rest args

:torso &rest args

:arms &rest args

:legs &rest args

:distribute-total-wrench-to-torque-method-default **

:joint-angle-limit-nspace-for-6dof &key (avoid-nspace-gain 0.01) (limbs ’(:rleg :lleg))

:joint-order limb &optional jname-list

:draw-gg-debug-view end-coords-list contact-state rz cog pz czmp dt

:footstep-parameter **

:make-support-polygons **

:make-sole-polygon name

:calc-zmp-from-forces-moments = `[method]
forces moments &key = (wrt :world) (limbs (if (send self :force-sensors) (remove nil (mapcar #’(lambda (fs) (find-if #’(lambda (l) (equal fs (car (send self l :force-sensors)))) ’(:rleg :lleg))) (send self :force-sensors))) ’(:rleg :lleg))) (force-sensors (mapcar #’(lambda (l) (car (send self l :force-sensors))) limbs)) (cop-coords (mapcar #’(lambda (l) (send self l :end-coords)) limbs)) (fz-thre 0.001) (limb-cop-fz-list (mapcar #’(lambda (fs f m cc) (let ((fsp (scale 0.001 (send fs :worldpos))) (nf (send fs :rotate-vector f)) (nm (send fs :rotate-vector m))) (send self :calc-cop-from-force-moment nf nm fs cc :fz-thre fz-thre :return-all-values t))) force-sensors forces moments cop-coords))
Calculate zmp[mm] from sensor local forces and moments
If force_z is large, zmp can be defined and returns 3D zmp.
Otherwise, zmp cannot be defined and returns nil.

:print-vector-for-robot-limb vec

Print angle vector with limb alingment and limb indent.
For example, if robot is rarm, larm, and torso, print result is:
#f(
rarm-j0 ... rarm-jN
larm-j0 ... larm-jN
torso-j0 ... torso-jN
)
:fullbody-inverse-kinematics = `[method]
target-coords &rest args &key = (move-target) (link-list) (min (float-vector -500 -500 -500 -20 -20 -10)) (max (float-vector 500 500 25 20 20 10)) (root-link-virtual-joint-weight #f(0.1 0.1 0.1 0.1 0.5 0.5)) (target-centroid-pos (apply #’midpoint 0.5 (send self :legs :end-coords :worldpos))) (cog-gain 1.0) (cog-translation-axis :z) (centroid-offset-func nil) (centroid-thre 5.0) (additional-weight-list) (joint-args nil) (cog-null-space nil) (min-loop 2) &allow-other-keys
fullbody inverse kinematics for legged robot.
necessary args : target-coords, move-target, and link-list must include legs’ (or leg’s) parameters
ex. (send robot:fullbody-inverse-kinematics (list rarm-tc rleg-tc lleg-tc) :move-target (list rarm-mt rleg-mt lleg-mt) :link-list (list rarm-ll rleg-ll lleg-ll))
:min
  lower position limit of root link virtual joint (x y z roll pitch yaw). Default is #f(-500[mm] -500[mm] -500[mm] -20[deg] -20[deg] -10[deg]).
:max
  upper position limit of root link virtual joint (x y z roll pitch yaw). Default is #f(500[mm] 500[mm] 25[mm] 20[deg] 20[deg] 10[deg]).
:root-link-virtual-joint-weight
  float-vector of inverse weight of velocity of root link virtual joint or a function which returns the float-vector (x y z roll pitch yaw). This works in the same way as :additional-weight-list in cascaded-coords::inverse-kinematics. Default is #f(0.1 0.1 0.1 0.1 0.5 0.5).
:joint-args
  list of other arguments passed to :init function of root link virtual joint (6dof-joint class).
   :max-joint-velocity
    limit of velocity of root link virtual joint (x y z roll pitch yaw). Default is #f((/ 0.08 0.05)[m/s] (/ 0.08 0.05)[m/s] (/ 0.08 0.05)[m/s] (/ pi 4)[rad/s] (/ pi 4)[rad/s] (/ pi 4)[rad/s]))
other-keys
  :fullbody-inverse-kinematics internally calls :inverse-kinematics and args are passed to it. See the explanation of :inverse-kinematics.
:calc-force-from-joint-torque = `[method]
limb all-torque &key = (move-target (send self limb :end-coords)) (use-torso)

Calculates end-effector force and moment from joint torques.

:torque-vector = `[method]
&key = (force-list) (moment-list) (target-coords) (debug-view nil) (calc-statics-p t) (dt 0.005) (av (send self :angle-vector)) (root-coords (send (car (send self :links)) :copy-worldcoords)) (calc-torque-buffer-args (send self :calc-torque-buffer-args)) (distribute-total-wrench-to-torque-method (if (and (not (every #’null (send self :legs))) (not (and force-list moment-list target-coords))) :distribute-total-wrench-to-torque-method-default))

Returns torque vector

:init-pose **

Set robot to initial posture.

:look-at-target look-at-target &key (target-coords)

move robot head to look at targets, look-at-target support t/nil float-vector coordinates, center of list of float-vector or list of coordinates

:inverse-kinematics-loop = `[method]
dif-pos dif-rot &rest args &key = target-coords debug-view look-at-target (move-target) (link-list (if (atom move-target) (send self :link-list (send move-target :parent)) (mapcar #’(lambda (mt) (send self :link-list (send mt :parent))) move-target))) &allow-other-keys
move move-target using dif-pos and dif-rot,
look-at-target suppots t, nil, float-vector, coords, list of float-vector, list of coords
link-list is set by default based on move-target ->root link link-list
:inverse-kinematics-loop internally calls :inverse-kinematics-loop function of cascaded-coords class. See the explanation of :inverse-kinematics-loop in cascaded-coords class.
:inverse-kinematics = `[method]
target-coords &rest args &key = look-at-target (move-target) (link-list (if (atom move-target) (send self :link-list (send move-target :parent)) (mapcar #’(lambda (mt) (send self :link-list (send mt :parent))) move-target))) &allow-other-keys
solve inverse kinematics, move move-target to target-coords
target-coords and move-target should be given.
link-list is set by default based on move-target ->root link link-list
:look-at-target
  target head looks at. This task is best-effort and only head joints are used. :look-at-target supports t, nil, float-vector, coords, list of float-vector, list of coords.
other-keys
  :inverse-kinematics internally calls :inverse-kinematics of cascaded-cords class and args are passed to it. See the explanation of :inverse-kinematics of cascaded-cords class.

:look-at-hand l/r

look at hand position, l/r supports :rarm, :larm, :arms, and ’(:rarm :larm)

:cameras **

Returns camera sensors.

:imu-sensors **

Returns imu sensors.

:force-sensors **

Returns force sensors.

:imu-sensor sensor-name

Returns imu sensor of given name

:force-sensor sensor-name

Returns force sensor with given name

:camera sensor-name

Returns camera with given name

:joint-order limb &optional jname-list

:joint-angle-limit-nspace-for-6dof &key (avoid-nspace-gain 0.01) (limbs ’(:rleg :lleg))

:distribute-total-wrench-to-torque-method-default **

:legs &rest args

:arms &rest args

:torso &rest args

:head &rest args

:rleg &rest args

:lleg &rest args

:rarm &rest args

:larm &rest args

:get-sensors-method-by-limb sensors-type limb

:get-sensor-method sensor-type sensor-name

:gripper limb &rest args

:inverse-kinematics-loop-for-look-at limb &rest args

:limb limb method &rest args

:torso-root-link **

:head-root-link **

:lleg-root-link **

:rleg-root-link **

:larm-root-link **

:rarm-root-link **

:torso-end-coords **

:head-end-coords **

:lleg-end-coords **

:rleg-end-coords **

:larm-end-coords **

:rarm-end-coords **

:init-ending **

:calc-static-balance-point = `[method]
&key = (target-points (mapcar #’(lambda (tmp-arm) (send (send self tmp-arm :end-coords) :worldpos)) ’(:rarm :larm))) (force-list (make-list (length target-points) :initial-element (float-vector 0 0 0))) (moment-list (make-list (length target-points) :initial-element (float-vector 0 0 0))) (static-balance-point-height (elt (apply #’midpoint 0.5 (send self :legs :end-coords :worldpos)) 2)) (update-mass-properties t)
Calculate static balance point which is equivalent to static extended ZMP.
The output is expressed by the world coordinates.
target-points are end-effector points on which force-list and moment-list apply.
force-list [N] and moment-list [Nm] are list of force and moment that robot receives at target-points.
static-balance-point-height is height of static balance point [mm].

:make-default-linear-link-joint-between-attach-coords attach-coords-0 attach-coords-1 end-coords-name linear-joint-name

Make default linear arctuator module such as muscle and cylinder and append lins and joint-list.
Module includes parent-link =>(j0) =>l0 =>(j1) =>l1 (linear actuator) =>(j2) =>l2 =>end-coords.
attach-coords-0 is root side coords which linear actulator is attached to.
attach-coords-1 is end side coords which linear actulator is attached to.
end-coords-name is the name of end-coords.
linear-joint-name is the name of linear actuator.

:support-polygon name

Return support polygon.
If name is list, return convex hull of all polygons.
Otherwise, return polygon with given name

:support-polygons **

Return support polygons.

:go-pos-quadruped-params->footstep-list xx yy th &key (type :crawl)

Calculate foot step list for quadruped walking from goal x position [mm], goal y position [mm], and goal yaw orientation [deg].

:go-pos-params->footstep-list = `[method]
xx yy th &key = ((:footstep-parameter prm) (send self :footstep-parameter)) ((:default-half-offset defp) (cadr (memq :default-half-offset prm))) ((:forward-offset-length xx-max) (cadr (memq :forward-offset-length prm))) ((:outside-offset-length yy-max) (cadr (memq :outside-offset-length prm))) ((:rotate-rad th-max) (abs (rad2deg (cadr (memq :rotate-rad prm))))) (gen-go-pos-step-node-func #’(lambda (mc leg leg-translate-pos) (let ((cc (send (send mc :copy-worldcoords) :translate (cadr (assoc leg leg-translate-pos))))) (send cc :name leg) cc)))

Calculate foot step list from goal x position [mm], goal y position [mm], and goal yaw orientation [deg].

:gen-footstep-parameter &key (ratio 1.0)

Generate footstep parameter

:calc-walk-pattern-from-footstep-list = `[method]
footstep-list &key = (default-step-height 50) (dt 0.1) (default-step-time 1.0) (solve-angle-vector-args) (debug-view nil) ((:all-limbs al) (if (send self :force-sensors) (remove nil (mapcar #’(lambda (fs) (find-if #’(lambda (l) (equal fs (car (send self l :force-sensors)))) ’(:rleg :lleg))) (send self :force-sensors))) ’(:rleg :lleg))) ((:default-zmp-offsets dzo) (mapcan #’(lambda (x) (list x (float-vector 0 0 0))) al)) (init-pose-function #’(lambda nil (send self :move-centroid-on-foot :both ’(:rleg :lleg)))) (start-with-double-support t) (end-with-double-support t) (ik-thre 1) (ik-rthre (deg2rad 1)) (q 1.0) (r 1.000000e-06) (calc-zmp t)
Calculate walking pattern from foot step list and return pattern list as a list of angle-vector, root-coords, time, and so on.
footstep-list should be given.
:footstep-list
  (list footstep1 footstep2 ...). :footstep-list can be any length. Each footstep indicates the destinations of swing legs in each step.
  footstep should be list of coordinate whose :name is identical with one swing leg and whose coords is the destination of that leg. If number of swing legs in a step is one, the footstep can be a coordinate.
  footstep1 is only for intialization and not executed.
:default-step-height
  Height of swing leg cycloid trajectories. Default is 50[mm].
:dt
  Sampling time of preview control and output walk pattern. Default is 0.1[s].
:default-step-time
  Reference time of each step. The first 10 percent and the last 10 percent of default-step-time is double support phase. Default is 1.0[s].
:solve-angle-vector-args
  :move-centroid-on-foot is used to solve IK in :calc-walk-pattern-from-footstep-list. :solve-angle-vector-args is passed to :move-centroid-on-foot in the form of (sendself :move-centroid-on-foot ... solve-angle-vector-args). Default is nil.
:debug-view
  Set t to show visualization. Default is nil.
:all-limbs
  list of limb names. In each walking step, limbs in :all-limbs but not assigned as swing legs by :footstep-list are considered to be support legs. Default is ’(:rleg :lleg) sorted in force-sensors order.
:default-zmp-offsets
  (list limbname1 offset1 limbname2 offset2 ...). :default-zmp-offsets should include every limb in :all-limbs. offset is a float-vector[mm] and local offset of reference zmp position from end-coords. Default offset is #F(0 0 0)[mm].
:init-pose-function
  A function which initialize robot’s pose. Walking pattern is generated from this initial pose. :init-pose-function is called once at the start of walking pattern generation in the form of (funcall init-pose-function). Default is #’(lambda () (send self :move-centroid-on-foot :both ’(:rleg :lleg))).
:start-with-double-support
  At the start of walking pattern generation, the initial position of reference zmp is
   t: midpoint of all-limbs.
   nil: midpoint of swing legs of footstep1.
  Default is t.
:end-with-double-support
  At the end of walking pattern generation, the final position of reference zmp is
   t: midpoint of all-limbs.
   nil: midpoint of support legs of the last footstep.
  Default is t.
:ik-thre
  Threshold for position error to terminate IK iteration. Default is 1[mm].
:ik-rthre
  Threshold for rotation error to terminate IK iteration. Default is (deg2rad 1)[rad].
:q
  Weight Q of the cost function of preview control. Default is 1.0.
:r
  Weight R of the cost function of preview control. Default is 1e-6.
:calc-zmp
  Set t to calculate resultant ZMP after IK. The calculated ZMP is visualized if :debug-view is t, and stored as czmp in return value. Default is t.
:move-centroid-on-foot = `[method]
leg fix-limbs &rest args &key = (thre (mapcar #’(lambda (x) (if (memq x ’(:rleg :lleg)) 1 5)) fix-limbs)) (rthre (mapcar #’(lambda (x) (deg2rad (if (memq x ’(:rleg :lleg)) 1 5))) fix-limbs)) (mid 0.5) (target-centroid-pos (if (eq leg :both) (apply #’midpoint mid (mapcar #’(lambda (tmp-leg) (send self tmp-leg :end-coords :worldpos)) (remove-if-not #’(lambda (x) (memq x ’(:rleg :lleg))) fix-limbs))) (send self leg :end-coords :worldpos))) (fix-limbs-target-coords (mapcar #’(lambda (x) (send self x :end-coords :copy-worldcoords)) fix-limbs)) (root-link-virtual-joint-weight #f(0.1 0.1 0.0 0.0 0.0 0.5)) &allow-other-keys
Move robot COG to change centroid-on-foot location,
leg : legs for target of robot’s centroid, which should be :both, :rleg, and :lleg.
fix-limbs : limb names which are fixed in this IK.
:fix-leg-to-coords = `[method]
fix-coords &optional (l/r :both) &key = (mid 0.5) &allow-other-keys
Fix robot’s legs to a coords
In the following codes, leged robot is assumed.

:foot-midcoords &optional (mid 0.5)

Calculate midcoords of :rleg and :lleg end-coords.
In the following codes, leged robot is assumed.

:make-sole-polygon name

:make-support-polygons **

:footstep-parameter **

:draw-gg-debug-view end-coords-list contact-state rz cog pz czmp dt

make-default-robot-link len radius axis name &optional extbody

センサモデル

sensor-model

:super = ** body**
:slots data profile

:init shape &key name &allow-other-keys

:draw-sensor v

:read **

:simulate model

:signal rawinfo

:profile &optional p

bumper-model

:super = ** sensor-model**
:slots bumper-threshold
:init = `[method]
b &rest args &key = ((:bumper-threshold bt) 20) name

Create bumper model, b is the shape of an object and bt is the threshold in distance[mm].

:simulate objs

Simulate bumper, with given objects, return 1 if the sensor detects an object and 0 if not.

:draw vwer

:draw-sensor vwer

:simulate objs

Simulate bumper, with given objects, return 1 if the sensor detects an object and 0 if not.

:init = `[method]
b &rest args &key = ((:bumper-threshold bt) 20) name

Create bumper model, b is the shape of an object and bt is the threshold in distance[mm].

:draw-sensor vwer

:draw vwer

camera-model

:super = ** sensor-model**
:slots (vwing :forward (:projection :newprojection :screen :view :viewpoint :view-direction :viewdistance :yon :hither)) img-viewer pwidth pheight
:init = `[method]
b &rest args &key = ((:width pw) 320) ((:height ph) 240) (view-up #f(0.0 1.0 0.0)) (viewdistance 100.0) (hither 100.0) (yon 10000.0) &allow-other-keys

Create camera model. b is the shape of an object

:create-viewer &optional cv &key (no-window nil)

Create camera viewer, or set viewer

:width **

Returns width of the camera in pixel.

:height **

Returns height of the camera in pixel.

:fovy **

Returns field of view in degree

:cx **

Returns center x.

:cy **

Returns center y.

:fx **

Returns focal length of x.

:fy **

Returns focal length of y.

:screen-point pos

Returns point in screen corresponds to the given pos.

:3d-point x y d

Returns 3d position

:ray x y

Returns ray vector of given x and y.

:draw-on = `[method]
&rest args &key = ((:viewer vwer) viewer) &allow-other-keys

Draw camera raw in irtviewer, ex (send cam :draw-on :flush t)

:draw-objects objs

Draw objects in camera viewer, expected type of objs is list of objects

:get-image = `[method]
&key = (with-points) (with-colors)

Get image objects you need to call :draw-objects before calling this function

:select-drawmode mode objs

Change drawmode for drawing with :draw-objects methods. mode is symbol of mode, ’hid is symbol for hidden line mode, the other symbols indicate default mode. objs is the same objects using :draw-objects.

:viewing &rest args

:image-viewer &rest args

:draw-sensor vwer &key flush (width 1) (color (float-vector 1 1 1))

:draw-objects-raw vwr objs

:get-image-raw vwr &key (points) (colors)

:select-drawmode mode objs

Change drawmode for drawing with :draw-objects methods. mode is symbol of mode, ’hid is symbol for hidden line mode, the other symbols indicate default mode. objs is the same objects using :draw-objects.

:get-image = `[method]
&key = (with-points) (with-colors)

Get image objects you need to call :draw-objects before calling this function

:draw-objects objs

Draw objects in camera viewer, expected type of objs is list of objects

:draw-on = `[method]
&rest args &key = ((:viewer vwer) viewer) &allow-other-keys

Draw camera raw in irtviewer, ex (send cam :draw-on :flush t)

:ray x y

Returns ray vector of given x and y.

:3d-point x y d

Returns 3d position

:screen-point pos

Returns point in screen corresponds to the given pos.

:fy **

Returns focal length of y.

:fx **

Returns focal length of x.

:cy **

Returns center y.

:cx **

Returns center x.

:fovy **

Returns field of view in degree

:height **

Returns height of the camera in pixel.

:width **

Returns width of the camera in pixel.

:create-viewer &optional cv &key (no-window nil)

Create camera viewer, or set viewer

:init = `[method]
b &rest args &key = ((:width pw) 320) ((:height ph) 240) (view-up #f(0.0 1.0 0.0)) (viewdistance 100.0) (hither 100.0) (yon 10000.0) &allow-other-keys

Create camera model. b is the shape of an object

:get-image-raw vwr &key (points) (colors)

:draw-objects-raw vwr objs

:draw-sensor vwer &key flush (width 1) (color (float-vector 1 1 1))

:image-viewer &rest args

:viewing &rest args

make-camera-from-param = `[function]
&key = pwidth pheight fx fy cx cy (tx 0) (ty 0) parent-coords name create-viewer (no-window nil)

Create camera object from given parameters.

環境モデル

scene-model

:super = ** cascaded-coords**
:slots name objs
:init = `[method]
&rest args &key = ((:name n) scene) ((:objects o)) ((:remove-wall w)) &allow-other-keys

Create scene model

:objects **

Returns objects in the scene.

:add-objects objects

Add objects to scene with identifiable names. Returns all objects.

:add-object obj

Add object to scene with identifiable name. Returns all objects.

:remove-objects objs-or-names

Remove objects or objects with given names from scene. Returns removed objects.

:remove-object obj-or-name

Remove object or object with given name from scene. Returns removed object.

:find-object name

Returns objects with given name.

:add-spots spots

Add spots to scene with identifiable names. All spots will be :assoc with this scene. Returns T if added spots successfly, otherwise returns NIL.

:add-spot spot

Add spot to scene with identifiable name. The spot will be :assoc with this scene. Returns T if spot is added successfly, otherwise returns NIL.

:remove-spots spots

Remove spots from this scene. All spots will be :dissoc with this scene. Returns removed spots.

:remove-spot spot

Remove spot from scene. the spot will be :dissoc with this scene. Returns removed spot.

:spots **

Return all spots in the scene.

:object name

Return an object of given name.

:spot name

Return a spot of given name.

:bodies **

:spot name

Return a spot of given name.

:object name

Return an object of given name.

:spots **

Return all spots in the scene.

:remove-spot spot

Remove spot from scene. the spot will be :dissoc with this scene. Returns removed spot.

:remove-spots spots

Remove spots from this scene. All spots will be :dissoc with this scene. Returns removed spots.

:add-spot spot

Add spot to scene with identifiable name. The spot will be :assoc with this scene. Returns T if spot is added successfly, otherwise returns NIL.

:add-spots spots

Add spots to scene with identifiable names. All spots will be :assoc with this scene. Returns T if added spots successfly, otherwise returns NIL.

:find-object name

Returns objects with given name.

:remove-object obj-or-name

Remove object or object with given name from scene. Returns removed object.

:remove-objects objs-or-names

Remove objects or objects with given names from scene. Returns removed objects.

:add-object obj

Add object to scene with identifiable name. Returns all objects.

:add-objects objects

Add objects to scene with identifiable names. Returns all objects.

:objects **

Returns objects in the scene.

:init = `[method]
&rest args &key = ((:name n) scene) ((:objects o)) ((:remove-wall w)) &allow-other-keys

Create scene model

:bodies **

動力学計算・歩行動作生成

歩行動作生成

歩行動作は予見制御を用いて生成される。文献 [15] [16] [17]_に述べられている式や文章を引用しつつ、説明する。

歩行動作は以下の手順で生成される。

  1. 脚の逆運動学が解ける範囲内の歩幅で、ロボットが足をつく位置と時間を計画する。
  2. 地面についていない足は、次につく位置までサイクロイド補間する。
  3. ZMPが地面についている足の位置とできる限り一致するような重心軌道を生成する。
  4. 計画された足と重心の軌道を満たすような関節角度軌道を逆運動学によって逐次求める。

ここでは、3の手順について詳しく説明する。

X方向の運動について、始めに次のような制御系を考える。Y方向の運動についても同様に議論することが可能である。

\[\begin{split}\begin{aligned} && \left\{ \begin{array}{l} x_{k+1} = A x_k + b u_k \\ p_k = c x_k \end{array} \right. \eqlabel{preview_control}\\ && x_k \equiv \left[ \begin{array}{c} x(k\Delta t)\\ \dot x(k\Delta t)\\ \ddot x(k\Delta t) \end{array} \right] ~~~~ u_k \equiv u(k\Delta t) ~~~~ p_k \equiv p(k\Delta t)\nonumber\\ && A \equiv \left[ \begin{array}{c c c} 1 & \Delta t & \Delta t^2 / 2\\ 0 & 1 & \Delta t\\ 0 & 0 & 1 \end{array} \right] ~~~~ b \equiv \left[ \begin{array}{c} \Delta t^3 / 6\\ \Delta t^2 / 2\\ \Delta t \end{array} \right] ~~~~ c \equiv \left[ \begin{array}{c c c} 1 & 0 & -z_c/g \end{array} \right]\nonumber\end{aligned}\end{split}\]

\(x\)はロボットの重心位置、\(u\)は重心の加速度の時間微分(jerk)、\(p\)はZMPである。

次に、このシステムを次のような拡大系に置き換える。

\[\begin{split}\begin{aligned} && \left\{ \begin{array}{l} x^\ast_{k+1} = \tilde{A} x^\ast_k + \tilde{b} \Delta u_k \\ p_k = \tilde{c} x^\ast_k \end{array} \right. \eqlabel{extended_preview_control}\\ && \Delta u_k \equiv u_k - u_{k-1} ~~~~ \Delta x_k \equiv x_k - x_{k-1} ~~~~ x^\ast_k \equiv \left[ \begin{array}{c} p_k\\ \Delta x_k \end{array} \right] \nonumber\\ && \tilde{A} \equiv \left[ \begin{array}{c c} 1 & cA\\ 0 & A \end{array} \right] ~~~~ \tilde{b} \equiv \left[ \begin{array}{c} cb\\ b \end{array} \right] ~~~~ \tilde{c} \equiv \left[ \begin{array}{c c c c} 1 & 0 & 0 & 0 \end{array} \right]\nonumber\end{aligned}\end{split}\]

こののシステムに対して、次のコスト関数を最小化するような制御入力を求める。

\[ \begin{align}\begin{aligned} \begin{aligned} J_k = \sum_{j=k}^{\infty} \{Q(p_{j}^{ref} - p_{j})^2 + R\Delta u_{j}^2\} \eqlabel{extended_preview_control_costfunc}\end{aligned}\\これは、以下のようにして求められる。\end{aligned}\end{align} \]

まず、十分大きい自然数\(M\)を用いて次のコスト関数を考え、次に\(M \rightarrow \infty\)とすることでを最小化する制御入力を得る。

\[\begin{aligned} J_k^M = \sum_{j=k}^{M-1} \{Q(p_{j}^{ref} - p_{j})^2 + R\Delta u_{j}^2\} \eqlabel{extended_preview_control_costfuncM}\end{aligned}\]

\(J_k^M\)の最小値を\(J_k^{M\ast}\)とすると、から次の関係が成り立つ。

\[ \begin{align}\begin{aligned} \begin{aligned} J_k^{M\ast} = \min_{\Delta u_k} \{Q(p_k^{ref} - p_k)^2 + R\Delta u_k^2 + J_{k+1}^{M\ast}\} \eqlabel{extended_preview_control_costfunc2}\end{aligned}\\ここで、\ :math:`J_k^{M\ast}`\ を次のようにおく。\end{aligned}\end{align} \]
\[\begin{aligned} J_k^{M\ast} = x_k^{\ast T} P_k^M x_k^\ast + \theta_k^{MT} x_k^\ast + \phi_k^M \eqlabel{extended_preview_control_J}\end{aligned}\]

これを用いて、の右辺を\(\Delta u_k\)で偏微分した値が0であることから、次の式を得る。

\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} 0 = && \frac{\partial}{\partial \Delta u_k} \{ Q(p_k^{ref} - p_k)^2 + R\Delta u_k^2 + (\tilde{A} x^\ast_k + \tilde{b} \Delta u_k)^T P_{k+1}^M (\tilde{A} x^\ast_k + \tilde{b} \Delta u_k) + \theta_{k+1}^{MT} (\tilde{A} x^\ast_k + \tilde{b} \Delta u_k) + \phi_{k+1}^M \} \nonumber\\ 0 =&& \Delta u_k^T R + \Delta u_k^T \tilde{b}^T P_{k+1}^M \tilde{b} + x_k^{\ast T} \tilde{A}^T P_{k+1}^M \tilde{b} + \frac{1}{2} \theta_{k+1}^{MT} \tilde{b} \nonumber \\ \Delta u_k =&& -(\tilde{b}^T P_{k+1}^M \tilde{b} + R )^{-1} \tilde{b}^T P_{k+1}^M \tilde{A} x_k^\ast - \frac{1}{2} (\tilde{b}^T P_{k+1}^M \tilde{b} + R )^{-1} \tilde{b}^T \theta_{k+1}^M\eqlabel{extended_preview_control_u}\end{aligned}\end{split}\\これをに代入することで、以下を得る。\end{aligned}\end{align} \]
\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} && x_k^{\ast T} P_k^M x_k^\ast + \theta_k^{M T} x_k^\ast + \phi_k^M \nonumber \\ =&& x_k^{\ast T} (\tilde{c}^T Q \tilde{c} + \tilde{A}^T P_{k+1}^M \tilde{A} - \tilde{A}^T P_{k+1}^M \tilde{b} (\tilde{b}^T P_{k+1}^M \tilde{b} + R )^{-1} \tilde{b}^T P_{k+1}^M \tilde{A}) x_k^\ast \nonumber\\ && + \{-2 \tilde{c}^T Q p_k^{ref} + \tilde{A}^T \theta_{k+1}^M - \tilde{A}^T P_{k+1}^M \tilde{b} (\tilde{b}^T P_{k+1}^M \tilde{b} + R )^{-1} \tilde{b}^T \theta_{k+1}^M \}^T x_k^\ast \nonumber\\ && + Q p_k^{ref 2} - \frac{1}{4} \theta_{k+1}^{MT} \tilde{b} (\tilde{b}^T P_{k+1}^M \tilde{b} + R )^{-1} \tilde{b}^T \theta_{k+1}^M + \phi_{k+1}^M\end{aligned}\end{split}\\これが任意の\ :math:`x_k^{\ast T}`\ に対し成り立つので、\end{aligned}\end{align} \]
\[\begin{split}\begin{aligned} P_k^M &=& \tilde{c}^T Q \tilde{c} + \tilde{A}^T P_{k+1}^M \tilde{A} - \tilde{A}^T P_{k+1}^M \tilde{b} (\tilde{b}^T P_{k+1}^M \tilde{b} + R )^{-1} \tilde{b}^T P_{k+1}^M \tilde{A} \eqlabel{extended_preview_control_P}\\ \theta_k^M &=& -2 \tilde{c}^T Q p_k^{ref} + \{\tilde{A}^T - \tilde{A}^T P_{k+1}^M \tilde{b} (\tilde{b}^T P_{k+1}^M \tilde{b} + R )^{-1} \tilde{b}^T\} \theta_{k+1}^M \eqlabel{extended_preview_control_theta}\\ \phi_k^M &=& Q p_k^{ref 2} - \frac{1}{4} \theta_{k+1}^{MT} \tilde{b} (\tilde{b}^T P_{k+1}^M \tilde{b} + R )^{-1} \tilde{b}^T \theta_{k+1}^M + \phi_{k+1}^M\end{aligned}\end{split}\]

境界条件を考えると、は\(k = M\)において\(J_{k+M}^{M\ast} = 0\)であるから、\(k = M\)においてが任意の\(x_{M}^\ast\)で恒等的に成り立つ条件を考えて、\(P_{M}^M = 0\)、\(\theta_{M}^M = 0\)、\(\phi_{M}^M = 0\)である。したがって、十分小さい\(j\)において\(P_{k+j}^M\)はの定常解\(P\)となり、次の式を満たす。

\[\begin{aligned} P &=& \tilde{c}^T Q \tilde{c} + \tilde{A}^T P \tilde{A} - \tilde{A}^T P \tilde{b} (\tilde{b}^T P \tilde{b} + R )^{-1} \tilde{b}^T P \tilde{A} \eqlabel{extended_preview_control_P2}\end{aligned}\]

以後、\(M \rightarrow \infty\)として考える。自然数\(N\)を考えて、\(j > N\)において\(p_{k+j}^{ref} = p_{k+N}^{ref}\)と仮定すると、は次のように表せる。(は十分小さい\(j\)における\(P_{k+j}\)でのみ成り立たつが、十分大きな\(j\)では\((\tilde{A} - \tilde{b} K)^{T j} \rightarrow 0\)と仮定し無視した。)(\(K \equiv (\tilde{b}^T P \tilde{b} + R )^{-1} \tilde{b}^T P \tilde{A}\)とおいた。)

\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} \theta_k &=& -2 \tilde{c}^T Q p_k^{ref} + (\tilde{A} - \tilde{b} K)^T \theta_{k+1} \nonumber\\ &=& -2 \{ \tilde{c}^T Q p_k^{ref} + (\tilde{A} - \tilde{b} K)^T \tilde{c}^T Q p_{k+1}^{ref} + \cdots + (\tilde{A} - \tilde{b} K)^{T N-2} \tilde{c}^T Q p_{k+N-1}^{ref} \nonumber\\ & & + (\tilde{A} - \tilde{b} K)^{T N-1} \tilde{c}^T Q p_{k+N}^{ref} + (\tilde{A} - \tilde{b} K)^{T N} \tilde{c}^T Q p_{k+N+1}^{ref} + (\tilde{A} - \tilde{b} K)^{T (N+1)} \tilde{c}^T Q p_{k+N+2}^{ref} + \cdots \} \nonumber \\ &=& -2 \{ \tilde{c}^T Q p_k^{ref} + (\tilde{A} - \tilde{b} K)^T \tilde{c}^T Q p_{k+1}^{ref} + \cdots + (\tilde{A} - \tilde{b} K)^{T N-2} \tilde{c}^T Q p_{k+N-1}^{ref} \nonumber\\ & & + (\tilde{A} - \tilde{b} K)^{T N-1} \tilde{c}^T Q p_{k+N}^{ref} + (\tilde{A} - \tilde{b} K)^{T N} \tilde{c}^T Q p_{k+N}^{ref} + (\tilde{A} - \tilde{b} K)^{T (N+1)} \tilde{c}^T Q p_{k+N}^{ref} + \cdots \} \nonumber \\ &=& -2 \sum_{j=1}^{N-1} \{ (\tilde{A} - \tilde{b} K)^{T j-1} \tilde{c}^T Q p_{k+j}^{ref} \} -2 \sum_{j=N}^{\infty} \{ (\tilde{A} - \tilde{b} K)^{T j-1} \tilde{c}^T Q p_{k+N}^{ref} \}\eqlabel{extended_preview_control_theta2}\end{aligned}\end{split}\\ここでを\ :math:`K`\ を用いて表現すると、\end{aligned}\end{align} \]
\[ \begin{align}\begin{aligned} \begin{aligned} P &=& \tilde{c}^T Q \tilde{c} + (\tilde{A} - \tilde{b} K)^T P \tilde{A} \eqlabel{extended_preview_control_P3}\end{aligned}\\が得られる。この両辺に\ :math:`P \tilde{A}`\ を加え整理すると、\end{aligned}\end{align} \]
\[\begin{aligned} (I - (\tilde{A} - \tilde{b} K)^{T}) P \tilde{A} &=& P (\tilde{A} - I) + \tilde{c}^T Q \tilde{c} \eqlabel{extended_preview_control_P4}\end{aligned}\]

となる。ここで\(\tilde{A} = \left[\begin{array}{c c} 1 & cA\\ 0 & A \end{array} \right]\)、\(\tilde{c} = \left[\begin{array}{c c c c} 1 & 0 & 0 & 0 \end{array} \right]\)を利用すると、の第1列目の等式から、

\[ \begin{align}\begin{aligned} \begin{aligned} (I - (\tilde{A} - \tilde{b} K)^{T}) P \tilde{c}^T &=& \tilde{c}^T Q \eqlabel{extended_preview_control_P5}\end{aligned}\\が成り立つ。このをに代入すると、\end{aligned}\end{align} \]
\[\begin{aligned} \theta_k &=& -2 \sum_{j=1}^{N-1} \{ (\tilde{A} - \tilde{b} K)^{T j-1} \tilde{c}^T Q p_{k+j}^{ref} \} -2 (\tilde{A} - \tilde{b} K)^{T N-1} P \tilde{c}^T p_{k+N}^{ref} \eqlabel{extended_preview_control_theta3}\end{aligned}\]

を得る。このをに代入することで、を最小化する最適制御入力\(\Delta u_k\)が得られる。

\[\begin{split}\begin{aligned} \Delta u_k &=& -K x_k^\ast + \sum_{j=1}^N \tilde{f}_j p_{k+j}^{ref}\eqlabel{extended_preview_control_u2}\\ \tilde{f}_j &=& \begin{cases} (\tilde{b}^T P \tilde{b} + R )^{-1} \tilde{b}^T (\tilde{A} - \tilde{b} K)^{T j-1} \tilde{c}^T Q & (j<N) \\ (\tilde{b}^T P \tilde{b} + R )^{-1} \tilde{b}^T (\tilde{A} - \tilde{b} K)^{T N-1} P \tilde{c}^T & (j=N) \end{cases}\nonumber\end{aligned}\end{split}\]

初期状態\(x_1^\ast\)と目標ZMP軌道\(p_{1}^{ref},~p_{2}^{ref},~\cdots\)が与えられれば、とのシステムによって\(\Delta u_1,~x_2^\ast,~\Delta u_2,~x_3^\ast,~\cdots\)が順次求まる。これによって、ZMPが地面についている足の位置とできる限り一致するような重心軌道を生成することができる。

歩行動作生成の例

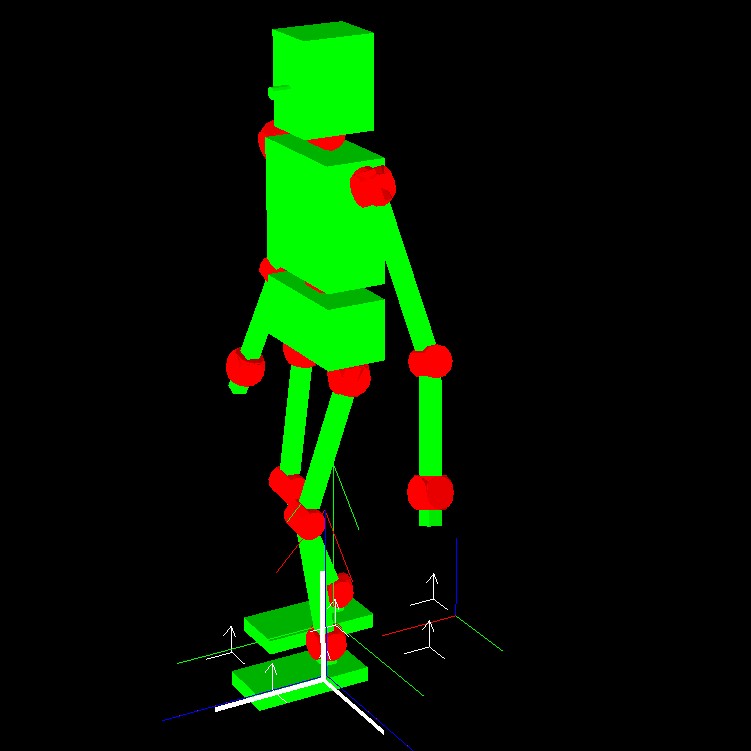
Example of walk pattern generation

Example of walk pattern generation

robot-modelクラスには、オフライン歩行動作生成を行い歩行軌道を返す関数:calc-walk-pattern-from-footstep-listが定義されている。この関数は、1歩ごとの足をつく位置のリストを与えると、ZMPがこの位置に出来る限り近くなるような歩行動作を生成する。以下に示すプログラムは、:calc-walk-pattern-from-footstep-listを用いて歩行動作生成を行うものである()。

(load "irteus/demo/sample-robot-model.l")
(setq *robot* (instance sample-robot :init))
(send *robot* :reset-pose)
(send *robot* :fix-leg-to-coords (make-coords))
(objects (list *robot*))

(let ((footstep-list
       (list (make-coords :coords (send *robot* :rleg :end-coords :copy-worldcoords) :name :rleg)
             (make-coords :coords (send (send *robot* :lleg :end-coords :copy-worldcoords)
                                        :translate #f(100 0 0)) :name :lleg)
             (make-coords :coords (send (send *robot* :rleg :end-coords :copy-worldcoords)
                                        :translate #f(200 0 0)) :name :rleg)
             (make-coords :coords (send (send *robot* :lleg :end-coords :copy-worldcoords)
                                        :translate #f(300 0 0)) :name :lleg)
             (make-coords :coords (send (send *robot* :rleg :end-coords :copy-worldcoords)
                                        :translate #f(400 0 0)) :name :rleg)
             (make-coords :coords (send (send *robot* :lleg :end-coords :copy-worldcoords)
                                        :translate #f(400 0 0)) :name :lleg))))
  (objects (append (list *robot*) footstep-list))

  (send *robot* :calc-walk-pattern-from-footstep-list
        footstep-list
        :default-step-height 50
        :default-step-time 1.0
        :dt 0.1
        :debug-view t)
  )

変数footstep-listに足をつく位置のリストをセットし、:calc-walk-pattern-from-footstep-listに与えている。footstep-listの各要素は、:nameにいずれの脚かを指定する必要がある。footstep-listの最初の要素は初期化のために用いられ、実際にロボットが脚を踏み出すのは次の要素以降の位置に対してである。:default-step-height 50では遊脚をサイクロイド補間するときの高さを50[mm]に指定している。:default-step-time 1.0は一歩あたりの時間を1.0[s]に指定している。:dt 0.1は予見制御のサンプリングタイムと生成される軌道の間隔を0.1[s]に指定している。なお、:default-step-height、:default-step-time、:dtはデフォルト値がこの値となっているため、実際にはこれらの値を設定する必要はない。

次に示すプログラムは、移動したい目的地を与えるとfootstep-listを自動で生成して歩行動作生成を行うものである。

(load "irteus/demo/sample-robot-model.l")
(setq *robot* (instance sample-robot :init))
(send *robot* :reset-pose)
(send *robot* :fix-leg-to-coords (make-coords))
(objects (list *robot*
               (apply #'midcoords 0.5 (send *robot* :legs :end-coords))
               (send (send (apply #'midcoords 0.5 (send *robot* :legs :end-coords))
                           :translate #F(500 150 0)) :rotate (deg2rad 45) :z)))

(send *robot* :calc-walk-pattern-from-footstep-list
      (send *robot* :go-pos-params->footstep-list
            500 150 45) ;; x[mm] y[mm] th[deg]
      :debug-view t
      )

footstep-listとして(send *robot* :go-pos-params->footstep-list 500 150 45)の返り値を与えて、先の例と同様:calc-walk-pattern-from-footstep-list関数で歩行動作を生成している。

:go-pos-params->footstep-list関数は、2本足で立ったロボットについて、脚の逆運動学が解ける範囲内で現在の位置から目的地までのfootstep-listを生成する関数であり、ここでは前に500[mm]、左に150[mm]移動し、左に45[deg]体を回転させるようなfootstep-listを生成している。

joint

:super = ** propertied-object**
:slots parent-link child-link joint-angle min-angle max-angle default-coords joint-velocity joint-acceleration joint-torque max-joint-velocity max-joint-torque joint-min-max-table joint-min-max-target

rotational-joint

:super = ** joint**
:slots parent-link child-link joint-angle min-angle max-angle default-coords joint-velocity joint-acceleration joint-torque max-joint-velocity max-joint-torque joint-min-max-table joint-min-max-target axis

linear-joint

:super = ** joint**
:slots parent-link child-link joint-angle min-angle max-angle default-coords joint-velocity joint-acceleration joint-torque max-joint-velocity max-joint-torque joint-min-max-table joint-min-max-target axis

omniwheel-joint

:super = ** joint**
:slots parent-link child-link joint-angle min-angle max-angle default-coords joint-velocity joint-acceleration joint-torque max-joint-velocity max-joint-torque joint-min-max-table joint-min-max-target axis

sphere-joint

:super = ** joint**
:slots parent-link child-link joint-angle min-angle max-angle default-coords joint-velocity joint-acceleration joint-torque max-joint-velocity max-joint-torque joint-min-max-table joint-min-max-target axis

6dof-joint

:super = ** joint**
:slots parent-link child-link joint-angle min-angle max-angle default-coords joint-velocity joint-acceleration joint-torque max-joint-velocity max-joint-torque joint-min-max-table joint-min-max-target axis

bodyset-link

:super = ** bodyset**
:slots rot pos parent descendants worldcoords manager changed geometry::bodies joint parent-link child-links analysis-level default-coords weight acentroid inertia-tensor angular-velocity angular-acceleration spacial-velocity spacial-acceleration momentum-velocity angular-momentum-velocity momentum angular-momentum force moment ext-force ext-moment

cascaded-link

:super = ** cascaded-coords**
:slots rot pos parent descendants worldcoords manager changed links joint-list bodies collision-avoidance-links end-coords-list

joint

:super = ** propertied-object**
:slots parent-link child-link joint-angle min-angle max-angle default-coords joint-velocity joint-acceleration joint-torque max-joint-velocity max-joint-torque joint-min-max-table joint-min-max-target

rotational-joint

:super = ** joint**
:slots parent-link child-link joint-angle min-angle max-angle default-coords joint-velocity joint-acceleration joint-torque max-joint-velocity max-joint-torque joint-min-max-table joint-min-max-target axis

linear-joint

:super = ** joint**
:slots parent-link child-link joint-angle min-angle max-angle default-coords joint-velocity joint-acceleration joint-torque max-joint-velocity max-joint-torque joint-min-max-table joint-min-max-target axis

bodyset-link

:super = ** bodyset**
:slots rot pos parent descendants worldcoords manager changed geometry::bodies joint parent-link child-links analysis-level default-coords weight acentroid inertia-tensor angular-velocity angular-acceleration spacial-velocity spacial-acceleration momentum-velocity angular-momentum-velocity momentum angular-momentum force moment ext-force ext-moment

cascaded-link

:super = ** cascaded-coords**
:slots rot pos parent descendants worldcoords manager changed links joint-list bodies collision-avoidance-links end-coords-list

:inertia-tensor &optional (update-mass-properties t)

Calculate total robot inertia tensor [g \(mm^2\)] around total robot centroid in euslisp world coordinates.
If update-mass-properties argument is t, propagate total mass prop calculation for all links and returns total robot inertia tensor.
Otherwise, do not calculate total mass prop, just returns pre-computed total robot inertia tensor.

:centroid &optional (update-mass-properties t)

Calculate total robot centroid (Center Of Gravity, COG) [mm] in euslisp world coordinates.
If update-mass-properties argument is t, propagate total mass prop calculation for all links and returns total robot centroid.
Otherwise, do not calculate total mass prop, just returns pre-computed total robot centroid.

:weight &optional (update-mass-properties t)

Calculate total robot weight [g].
If update-mass-properties argument is t, propagate total mass prop calculation for all links and returns total robot weight.
Otherwise, do not calculate total weight, just returns pre-computed total robot weight.
:calc-zmp = `[method]
&optional (av (send self :angle-vector)) (root-coords (send (car (send self :links)) :copy-worldcoords)) &key = (pzmpz 0.0) (dt 0.005) (update t) (debug-view) (calc-torque-buffer-args (send self :calc-torque-buffer-args))
Calculate Zero Moment Point based on Inverse Dynamics.
The output is expressed by the world coordinates,
and depends on historical robot states of the past 3 steps. Step is incremented when this method is called.
After solving Inverse Dynamics, ZMP is calculated from total root-link force and moment.
necessary arguments ->av and root-coords.
If update is t, call inverse dynamics, otherwise, just return zmp from total root-link force and moment.
dt [s] is time step used only when update is t.
pZMPz is ZMP height [mm].
After this method, (send robot :get :zmp) is ZMP and (send robot :get :zmp-moment) is moment around ZMP.

:preview-control-dynamics-filter dt avs &key (preview-controller-class preview-controller) (cog-method :move-base-pos) (delay 0.8)

:draw-torque vwer &key flush (width 2) (size 100) (color (float-vector 1 0.3 0)) (warning-color (float-vector 1 0 0)) (torque-threshold nil) (torque-vector (send self :torque-vector)) ((:joint-list jlist) (send self :joint-list))

:calc-contact-wrenches-from-total-wrench target-pos-list &key (total-wrench) (weight (fill (instantiate float-vector (6 (length target-pos-list))) 1))

:wrench-list->wrench-vector wrench-list

:wrench-vector->wrench-list wrench-vector

:calc-cop-from-force-moment force moment sensor-coords cop-coords &key (fz-thre 1) (return-all-values)

:calc-torque-from-ext-wrenches &key (force-list) (moment-list) (target-coords) ((:jacobi tmp-jacobi))

:calc-av-vel-acc-from-pos dt av

:calc-root-coords-vel-acc-from-pos dt root-coords

:calc-torque-from-vel-acc &key (debug-view nil) (jvv (instantiate float-vector (length joint-list))) (jav (instantiate float-vector (length joint-list))) (root-spacial-velocity (float-vector 0 0 0)) (root-angular-velocity (float-vector 0 0 0)) (root-spacial-acceleration (float-vector 0 0 0)) (root-angular-acceleration (float-vector 0 0 0)) (calc-torque-buffer-args (send self :calc-torque-buffer-args))

:calc-torque-without-ext-wrench &key (debug-view nil) (calc-statics-p t) (dt 0.005) (av (send self :angle-vector)) (root-coords (send (car (send self :links)) :copy-worldcoords)) (calc-torque-buffer-args (send self :calc-torque-buffer-args))

:calc-torque &key (debug-view nil) (calc-statics-p t) (dt 0.005) (av (send self :angle-vector)) (root-coords (send (car (send self :links)) :copy-worldcoords)) (force-list) (moment-list) (target-coords) (calc-torque-buffer-args (send self :calc-torque-buffer-args))

:calc-torque-buffer-args **

:torque-ratio-vector &rest args &key (torque (sendself :torque-vector args))

:max-torque-vector **

riccati-equation

:super = ** propertied-object**
:slots a b c p q r k a-bkt r+btpb-1

:solve **

:init aa bb cc qq rr

preview-controller

:super = ** riccati-equation**
:slots xk uk delay f1-n y1-n queue-index initialize-queue-p additional-data-queue finishedp initialized-p output-dim input-dim
:init = `[method]
dt &key = (q) (r) ((:delay d)) ((:a _a)) ((:b _b)) ((:c _c)) (state-dim (array-dimension _a 0)) ((:output-dim odim) (array-dimension _c 0)) ((:input-dim idim) (array-dimension _b 1)) (init-xk (instantiate float-vector (array-dimension _a 0))) (init-uk (make-matrix (array-dimension _b 1) 1)) ((:initialize-queue-p iqp))
Initialize preview-controller.
Q is weighting of output error and R is weighting of input.
dt is sampling time [s].
delay is preview time [s].
init-xk is initial state value.
A, B, C are state eq matrices.
If initialize-queue-p is t, fill all queue by the first input at the begenning, otherwise, do not fill queue at the first.

:update-xk p &optional (add-data)

Update xk by inputting reference output.
Return value : nil (initializing) =>return values (middle) =>nil (finished)
If p is nil, automatically the last value in queue is used as input and preview controller starts finishing.

:finishedp **

Finished or not.

:last-reference-output-vector **

Last value of reference output queue vector (y_k+N_ref).
Last value is latest future value.

:current-reference-output-vector **

First value of reference output queue vector (y_k_ref).
First value is oldest future value and it can be used as current reference value.

:current-state-vector **

Current state value (xk).

:current-output-vector **

Current output value (yk).

:current-additional-data **

Current additional data value.
First value of additional-data-queue.

:pass-preview-controller reference-output-vector-list

Get preview controller results from reference-output-vector-list and returns list.

:calc-f **

:calc-u **

:calc-xk **

:pass-preview-controller reference-output-vector-list

Get preview controller results from reference-output-vector-list and returns list.

:current-additional-data **

Current additional data value.
First value of additional-data-queue.

:current-output-vector **

Current output value (yk).

:current-state-vector **

Current state value (xk).

:current-reference-output-vector **

First value of reference output queue vector (y_k_ref).
First value is oldest future value and it can be used as current reference value.

:last-reference-output-vector **

Last value of reference output queue vector (y_k+N_ref).
Last value is latest future value.

:finishedp **

Finished or not.

:update-xk p &optional (add-data)

Update xk by inputting reference output.
Return value : nil (initializing) =>return values (middle) =>nil (finished)
If p is nil, automatically the last value in queue is used as input and preview controller starts finishing.
:init = `[method]
dt &key = (q) (r) ((:delay d)) ((:a _a)) ((:b _b)) ((:c _c)) (state-dim (array-dimension _a 0)) ((:output-dim odim) (array-dimension _c 0)) ((:input-dim idim) (array-dimension _b 1)) (init-xk (instantiate float-vector (array-dimension _a 0))) (init-uk (make-matrix (array-dimension _b 1) 1)) ((:initialize-queue-p iqp))
Initialize preview-controller.
Q is weighting of output error and R is weighting of input.
dt is sampling time [s].
delay is preview time [s].
init-xk is initial state value.
A, B, C are state eq matrices.
If initialize-queue-p is t, fill all queue by the first input at the begenning, otherwise, do not fill queue at the first.

:calc-xk **

:calc-u **

:calc-f **

extended-preview-controller

:super = ** preview-controller**
:slots orga orgb orgc xk
:init = `[method]
dt &key = (q) (r) ((:delay d)) ((:a _orga)) ((:b _orgb)) ((:c _orgc)) (init-xk (instantiate float-vector (array-dimension _orga 0))) (init-uk (make-matrix (array-dimension _orgb 1) 1)) (state-dim (array-dimension _orga 0)) ((:initialize-queue-p iqp)) (q-mat)
Initialize preview-controller in extended system (error system).
Q is weighting of output error and R is weighting of input.
dt is sampling time [s].
delay is preview time [s].
init-xk is initial state value.
A, B, C are state eq matrices for original system and slot variables A,B,C are used for error system matrices.
If initialize-queue-p is t, fill all queue by the first input at the begenning, otherwise, do not fill queue at the first.

:current-output-vector **

Current additional data value.
First value of additional-data-queue.

:calc-f **

:calc-u **

:calc-xk **

:current-output-vector **

Current additional data value.
First value of additional-data-queue.
:init = `[method]
dt &key = (q) (r) ((:delay d)) ((:a _orga)) ((:b _orgb)) ((:c _orgc)) (init-xk (instantiate float-vector (array-dimension _orga 0))) (init-uk (make-matrix (array-dimension _orgb 1) 1)) (state-dim (array-dimension _orga 0)) ((:initialize-queue-p iqp)) (q-mat)
Initialize preview-controller in extended system (error system).
Q is weighting of output error and R is weighting of input.
dt is sampling time [s].
delay is preview time [s].
init-xk is initial state value.
A, B, C are state eq matrices for original system and slot variables A,B,C are used for error system matrices.
If initialize-queue-p is t, fill all queue by the first input at the begenning, otherwise, do not fill queue at the first.

:calc-xk **

:calc-u **

:calc-f **

preview-control-cart-table-cog-trajectory-generator

:super = ** propertied-object**
:slots pcs cog-z zmp-z
:init = `[method]
dt _zc &key = (q 1) (r 1.000000e-06) ((:delay d) 1.6) (init-xk (float-vector 0 0 0)) ((:a _a) (make-matrix 3 3 (list (list 1 dt (0.5 dt dt)) (list 0 1 dt) (list 0 0 1)))) ((:b _b) (make-matrix 3 1 (list (list ((/ 1.0 6.0) dt dt dt)) (list (0.5 dt dt)) (list dt)))) ((:c _c) (make-matrix 1 3 (list (list 1.0 0.0 (- (/ _zc (elt g-vec2))))))) ((:initialize-queue-p iqp)) (preview-controller-class extended-preview-controller)
COG (xy) trajectory generator using preview-control convert reference ZMP from reference COG.
dt ->sampling time[s], _zc is height of COG [mm].
preview-controller-class is preview controller class (extended-preview-controller by default).
For other arguments, please see preview-controller and extended-preview-controller :init documentation.

:refcog **

Reference COG [mm].

:cart-zmp **

Cart-table system ZMP[mm] as an output variable.

:last-refzmp **

Reference zmp at the last of queue.

:current-refzmp **

Current reference zmp at the first of queue.

:update-xk p &optional (add-data)

Update xk and returns zmp and cog values.
For arguments, please see preview-controller and extended-preview-controller :update-xk.

:finishedp **

Finished or not.

:current-additional-data **

Current additional data value.

:pass-preview-controller reference-output-vector-list

Get preview controller results from reference-output-vector-list and returns list.

:cog-z **

COG Z [mm].

:update-cog-z zc

:cog-z **

COG Z [mm].

:pass-preview-controller reference-output-vector-list

Get preview controller results from reference-output-vector-list and returns list.

:current-additional-data **

Current additional data value.

:finishedp **

Finished or not.

:update-xk p &optional (add-data)

Update xk and returns zmp and cog values.
For arguments, please see preview-controller and extended-preview-controller :update-xk.

:current-refzmp **

Current reference zmp at the first of queue.

:last-refzmp **

Reference zmp at the last of queue.

:cart-zmp **

Cart-table system ZMP[mm] as an output variable.

:refcog **

Reference COG [mm].

:init = `[method]
dt _zc &key = (q 1) (r 1.000000e-06) ((:delay d) 1.6) (init-xk (float-vector 0 0 0)) ((:a _a) (make-matrix 3 3 (list (list 1 dt (0.5 dt dt)) (list 0 1 dt) (list 0 0 1)))) ((:b _b) (make-matrix 3 1 (list (list ((/ 1.0 6.0) dt dt dt)) (list (0.5 dt dt)) (list dt)))) ((:c _c) (make-matrix 1 3 (list (list 1.0 0.0 (- (/ _zc (elt g-vec2))))))) ((:initialize-queue-p iqp)) (preview-controller-class extended-preview-controller)
COG (xy) trajectory generator using preview-control convert reference ZMP from reference COG.
dt ->sampling time[s], _zc is height of COG [mm].
preview-controller-class is preview controller class (extended-preview-controller by default).
For other arguments, please see preview-controller and extended-preview-controller :init documentation.

:update-cog-z zc

gait-generator

:super = ** propertied-object**
:slots robot dt footstep-node-list support-leg-list support-leg-coords-list swing-leg-dst-coords-list swing-leg-src-coords refzmp-cur-list refzmp-next refzmp-prev step-height-list one-step-len index-count default-step-height default-double-support-ratio default-zmp-offsets finalize-p apreview-controller all-limbs end-with-double-support ik-thre ik-rthre swing-leg-proj-ratio-interpolation-acc swing-leg-proj-ratio-interpolation-vel swing-leg-proj-ratio-interpolation-pos swing-rot-ratio-interpolation-acc swing-rot-ratio-interpolation-vel swing-rot-ratio-interpolation-pos

:cycloid-midcoords ratio start goal height &key (top-ratio 0.5) (rot-ratio ratio)

:cycloid-midpoint ratio start goal height &key (top-ratio 0.5)

:solve-av-by-move-centroid-on-foot support-leg support-leg-coords swing-leg-coords cog robot &rest args &key (cog-gain 3.5) (stop 100) (additional-nspace-list) &allow-other-keys

:solve-angle-vector support-leg support-leg-coords swing-leg-coords cog &key (solve-angle-vector :solve-av-by-move-centroid-on-foot) (solve-angle-vector-args)

:update-current-gait-parameter **

:proc-one-tick &key (type :shuffling) (solve-angle-vector :solve-av-by-move-centroid-on-foot) (solve-angle-vector-args) (debug nil)

:calc-one-tick-gait-parameter type

:calc-current-refzmp prev cur next

:calc-ratio-from-double-support-ratio **

:calc-current-swing-leg-coords ratio src dst &key (type :shuffling) (step-height default-step-height)

:calc-hoffarbib-pos-vel-acc tmp-remain-time tmp-goal old-acc old-vel old-pos

:make-gait-parameter **

:finalize-gait-parameter **

:initialize-gait-parameter fsl time cog &key ((:default-step-height dsh) 50) ((:default-double-support-ratio ddsr) 0.2) (delay 1.6) ((:all-limbs al) ’(:rleg :lleg)) ((:default-zmp-offsets dzo) (mapcan #’(lambda (x) (list x (float-vector 0 0 0))) al)) (q 1.0) (r 1.000000e-06) (thre 1) (rthre (deg2rad 1)) (start-with-double-support t) ((:end-with-double-support ewds) t)

:get-swing-limbs limbs

:get-limbs-zmp limb-coords limb-names

:get-limbs-zmp-list limb-coords limb-names

:get-counter-footstep-limbs fs

:get-footstep-limbs fs

:init rb _dt

calc-inertia-matrix-rotational mat row column paxis m-til c-til i-til axis-for-angular child-link world-default-coords translation-axis rotation-axis tmp-v0 tmp-v1 tmp-v2 tmp-va tmp-vb tmp-vc tmp-vd tmp-m

calc-inertia-matrix-linear mat row column paxis m-til c-til i-til axis-for-angular child-link world-default-coords translation-axis rotation-axis tmp-v0 tmp-v1 tmp-v2 tmp-va tmp-vb tmp-vc tmp-vd tmp-m

[1]Inverse kinematic solutions with singularity robustness for robot manipulator control: Y.Nakamura and H. Hanafusa, Journal of Dynamic Systems, Measurement, and Control, vol. 108, pp 163-171, 1986
[2]ロボットアームの可操作度, 吉川恒夫, 日本ロボット学会誌, vol. 2, no. 1, pp. 63-67, 1984.
[3]Hybrid Position/Force Control: A Correct Formuration, William D. Fisher, M. Shahid Mujtaba, The Internationaltional Journal of Robotics Research, vol. 11, no. 4, pp. 299-311, 1992.
[4]A unified approach for motion and force control of robot manipulators: The operational space formulation, O. Khatib, IEEE Journal of Robotics and Automation, vol. 3, no. 1, pp. 43-53, 1987.
[5]Exploiting Task Intervals for Whole Body Robot Control, Michael Gienger and Herbert Jansen and Christian Goeric In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’06), pp. 2484 - 2490, 2006
[6]A weighted least-norm solution based scheme for avoiding jointlimits for redundant joint manipulators, Tan Fung Chan and Dubey R.V., Robotics and Automation, IEEE Transactions on, pp. 286-292,1995
[7]Efficient gradient projection optimization for manipulators withmultiple degrees of redundancy, Zghal H., Dubey R.V., Euler J.A., 1990 IEEE International Conference on Robotics and Automation, pp. 1006-1011, 1990.
[8]Real-Time Self Collision Avoidance for Humanoids by means of Nullspace Criteria and Task Intervals, H. Sugiura, M. Gienger, H. Janssen, C. Goerick, Proceedings of the 2006 IEEE-RAS International Conference on Humanoid Robots, pp. 575-580, 2006.
[9]Real-time collision avoidance with whole body motion control for humanoid robots, Hisashi Sugiura, Michael Gienger, Herbert Janssen, Christian Goerick, In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’07), pp. 2053 - 2068, 2007
[10]Fast distance queries with rectangular swept sphere volumes, Larsen E., Gottschalk S., Lin M.C., Manocha D, Proceedings of The 2000 IEEE International Conference on Robotics and Automation, pp. 3719-3726, 2000.
[11]アーム・多指ハンド機構による把握と操り, 永井 清, 吉川 恒夫, 日本ロボット学会誌, vol. 13, no. 7, pp. 994-1005, 1995.
[12]一般化ヤコビ行列を用いた宇宙用ロボットマニピュレータの分解速度制御, 梅谷 陽二, 吉田 和哉, 日本ロボット学会誌, vol. 4, no. 7, pp. 63-73, 1989.
[13]Control of Free-Floating Humanoid Robots Through Task Prioritization, Luis Sentis and Oussama Khatib, Proceedings of The 2005 IEEE International Conference on Robotics and Automation, pp. 1718-1723, 2005
[14]Resolved Momentum Control:Humanoid Motion Planning based on the Linear and Angular Momentum, S.Kajita, F.Kanehiro, K.Kaneko, K.Fujiwara, K.Harada, K.Yokoi,H.Hirukawa, In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’03), pp. 1644-1650, 2003
[15]Humanoid Robot (in Japanese), Shuji Kajita, Ohmsha, 2005, ISBN 4-274-20058-2
[16]Biped Walking Pattern Generation by using Preview Control of Zero-Moment Point, Shuji Kajita and Fumio Kanehiro and Kenji Kaneko and Kiyoshi Fujiwara and Kensuke Harada and Kazuhito Yokoi and Hirohisa Hirukawa, ICRA 2003, p.1620-1626, 2006
[17]最適予見制御と一般化予測制御, 江上 正 and土谷 武士, 計測と制御, 39 巻, 5 号, p.337-342, 2000